Understanding 2D Physics Engines with Phaser 3, Part 9: Capsule to Capsule Collision and Resolution
- cedarcantab
- Mar 21, 2022
- 5 min read
Updated: May 15, 2023
Capsules
Phaser 3's default arcade physics engine handles physics bodies as either rectangles (AABB only) or circles. It appears that in the physics engine world, there is another popular shape used for physis bodies called capsules, which is what this post is about.

Defining a capsule
This article here explains in great detail what capsules are. In essence, it is two circles joined by two lines.
There are lots of different ways of defining such a shape with different merits and demerits.
Definition 1
One common way of defining a capsule is by specifying the "major" and "minor" radii.

The key properties are:
center = (x,y)
cap radius = (major - minor) / 2
centers of the caps = (x-(major - minor) / 2, y) and ( x+(major - minor) / 2, y)
Definition 2
I have create my own version of a Capsules class by extending Phaser 3's line class, which requires the ends of the "segment" to be defined as (x1, y1) and (x2, y2).
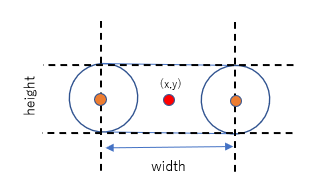
I have decided to pass in the "centre" of the capsule (shown in red above) as x,y, the "width" of the capsule (i.e. the distance from the centers of the end caps), and the "height".
The key properties are:
center = (x,y)
cap radius = height / 2
centers of the caps = (x-width/2, y) and (x+width/2, y)
The constructor, update, translate and rotate methods are pretty much the same as polygons.
class Capsule extends Phaser.Geom.Line {
constructor(scene, x, y, w, h) {
super(x-w/2+h/2, y, x + w/2-h/2, y)
this.scene = scene;
// linear components
this.position = new Phaser.Math.Vector2((this.x1 + this.x2)/2, (this.y1+this.y2)/2);
this.velocity = new Phaser.Math.Vector2();
this.velocityDelta = new Phaser.Math.Vector2();
this.maxSpeed = 100;
this.acceleration = new Phaser.Math.Vector2();
// angular components
this.angle = 0;
this.direction = new Phaser.Math.Vector2(1,0);
this.angularVelocity = 0;
this.angularDelta = 0;
this.angularAcceleration = 0;
// material components
this.length = w;
this.height = h;
this.radius = h/2;
this.area = this.radius*2*Phaser.Geom.Line.Length(this)+Math.PI*this.radius*this.radius;
this.density = 0.01;
this.mass = this.area*this.density;
this.inverse_mass = this.mass === 0 ? 0 : 1 / this.mass;
this.restitution = 1;
this.isStatic = false;
this.isColliding = false;
this.color = white; // default color is white
}
update(dt) {
this.velocity.add(this.acceleration.clone().scale(dt));
this.velocity.limit(this.maxSpeed);
this.velocityDelta.set(this.velocity.x*dt, this.velocity.y*dt);
this.translate(this.velocityDelta);
this.angularVelocity += this.angularAcceleration*dt;
this.angularVeloctiy = Phaser.Math.Clamp(this.angularVelocity, -Math.PI/4,Math.PI/4);
this.angularDelta = this.angularVelocity*dt;
this.rotate(this.angularDelta)
}
translate(delta) {
Phaser.Geom.Line.Offset(this, delta.x, delta.y);
this.position.set((this.x1+this.x2)/2, (this.y1+this.y2)/2)
}
rotate(angle) {
Phaser.Geom.Line.Rotate(this, angle);
this.angle = Phaser.Geom.Line.Angle(this);
this.direction.setAngle(this.angle);
}
The rendering of the object is a little tricky, since it involves drawing semi-circles at each end - need a bit of tinkering to get the start and end angles correct.
render() {
if (this.isColliding) {
this.scene.graphics.lineStyle(1, red);
} else {
this.scene.graphics.lineStyle(1, this.color);
}
this.scene.graphics.beginPath();
this.scene.graphics.arc(this.x1, this.y1, this.radius, Math.PI/2 + this.angle, -Math.PI/2 + this.angle);
this.scene.graphics.lineTo(this.x2 + this.radius * Phaser.Geom.Line.NormalX(this), this.y2 + this.radius * Phaser.Geom.Line.NormalY(this));
this.scene.graphics.arc(this.x2, this.y2, this.radius, -Math.PI/2+this.angle, Math.PI/2+this.angle);
this.scene.graphics.closePath()
this.scene.graphics.strokePath();
}Collision Detection
Collision detection between two capsules is an extension of the circle to circle intersection test. You need to find the closest point from the centres of the circles of one capsule to the "axis" of the other capsule, and vice versa, then take the shortest distance. The vector connecting the relevant circle centre and the nearest point on the axis of the other capsule is the minimum translation vector.
We already know how to find the nearest point on a line segment from a point (a slight amendment of the similar method from Phaser). Below is the code which finds the nearest point on a segment and returns the distance, and the normal (ie the vector from the point and the nearest point on the line).
nearestPointOnLine(point, line) {
//returns with the closest point on a line segment to the centre of circle
let out = new Phaser.Geom.Point();
let x1 = line.x1;
let y1 = line.y1;
let x2 = line.x2;
let y2 = line.y2;
let L2 = (((x2 - x1) * (x2 - x1)) + ((y2 - y1) * (y2 - y1)));
let r = (((point.x - x1) * (x2 - x1)) + ((point.y - y1) * (y2 - y1))) / L2;
r = Phaser.Math.Clamp(r, 0, 1);
out.x = x1 + (r * (x2 - x1));
out.y = y1 + (r * (y2 - y1));
let dist =Phaser.Math.Distance.BetweenPoints(out,point);
this.graphics.lineBetween(point.x,point.y,out.x, out.y);
return {dist: dist, normal: new Phaser.Math.Vector2(point.x-out.x, point.y-out.y)}
};The following code, whilst not particularly compact, is hopefully easy to follow. In the red highlighted code, each of the centres of capsule A are tested against capsule B, and the closest capsule A centre and the nearest point on capsule B is stored in variable closestPoints.
Then the same check is performed the other way around; ie the centres of capsule B are checked against capsule A. If a closer pair of points are found (ie a centre of capsule B and some point on capsule A), then the new pair is stored in variable closestPoints, ensuring that the point of capsule A is stored first in the closetPoints array.
Being consistent in the order in which the points are returned is important, as we will need to be consistent in the direction of the collision normal.
distanceBetweenCapsules(capsuleA, capsuleB) {
let checkPair;
checkPair = this.nearestPointOnLine(capsuleA.getPointA(), capsuleB);
let shortestDist = checkPair.dist;
let closestPoints = [capsuleA.getPointA(), checkPair.point];
checkPair = this.nearestPointOnLine(capsuleA.getPointB(), capsuleB);
if (checkPair.dist<shortestDist) {
shortestDist = checkPair.dist;
closestPoints = [capsuleA.getPointB(), checkPair.point];
}
checkPair = this.nearestPointOnLine(capsuleB.getPointA(), capsuleA);
if (checkPair.dist<shortestDist) {
shortestDist = checkPair.dist;
closestPoints = [checkPair.point, capsuleB.getPointA()]
}
checkPair = this.nearestPointOnLine(capsuleB.getPointB(), capsuleA);
if (checkPair.dist<shortestDist) {
shortestDist = checkPair.dist;
closestPoints = [checkPair.point, capsuleB.getPointB()]
}
return {distance: shortestDist, points: closestPoints}
}With this information, it is just a matter of now carrying out the standard circle to circle collision test.
intersectCaps2Caps(capsuleA, capsuleB, manifold) {
let {distance: distance, points: PT} = this.distanceBetweenCapsules(capsuleA, capsuleB);
if (distance <= (capsuleA.radius+capsuleB.radius)) {
manifold.depth = (capsuleA.radius+capsuleB.radius) - distance
manifold.normal = new Phaser.Math.Vector2(PT[0].x-PT[1].x, PT[0].y-PT[1].y).normalize();
return true;
}
else
{
return null
}
}Alternate way to code the collision detection
I did code the collision detection in the following way, where I store all the distances of the 4 checks in an array, and loop through it. With this method I have to check which "combination" points and reverse the normal vector direction. Is it more elegant? I am not sure..
intersectCaps2Caps(capsuleA, capsuleB, manifold) {
let distance = Number.MAX_VALUE;
let normal = new Phaser.Math.Vector2(1,0);
let cp = new Phaser.Geom.Point()
let separation = [
this.nearestPointOnLine(capsuleB.getPointA(), capsuleA),
this.nearestPointOnLine(capsuleB.getPointB(), capsuleA),
this.nearestPointOnLine(capsuleA.getPointA(), capsuleB),
this.nearestPointOnLine(capsuleA.getPointB(), capsuleB)
];
for (let i = 0; i<separation.length; i++) {
if (separation[i].dist<distance) {
distance = separation[i].dist;
if (i<=1) {
normal = separation[i].normal
} else
{
normal = separation[i].normal.negate();
}
}
}
manifold.normal = normal.normalize();
manifold.depth = distance - (capsuleA.radius+capsuleB.radius);
return (manifold.depth <= 0)
}
Collision Separation
Having got this far, it is easy to build the collision separation code (without rotation).
It took me literally hours to figure out that I had forgotten to include the clone() after the normal in the below code, trying to figure out why the collision would not work properly.
resolveCaps2Caps2(capsuleA, capsuleB, manifold) {
let sepFactor = manifold.depth / (capsuleA.inverse_mass + capsuleB.inverse_mass);
capsuleA.translate(manifold.normal.clone().scale(capsuleA.inverse_mass*sepFactor));
capsuleB.translate(manifold.normal.clone().negate().scale(capsuleB.inverse_mass*sepFactor));
}


Comments