Extending Box2D-Lite in Javascript: Support Point based SAT

Separating Axis Theorem utilising Support Points

In my various implementations of the separating axis theorem for detecting collision between shapes, I have adopted the approach of projecting the vertices of both the shapes onto the outward facing normals of both shapes, and looking for overlaps of the resulting intervals.

This post describes a slightly different way of implementing the separating axis theorem; one that utilizes support points.

The fundamental idea behind the SAT is to assess whether there exists an "axis" that separates the two shapes. The concept is easy but the tricky part is the algorithm for efficiently looking for such an axis (or assessing that such an axis does not exist), given that there are in theory infinite number of potential axes to check.

One way is to check through the outward facing normals of each shape.

Another way explained in this tutorial here, is to build a plane for each face / edge of the shapes, finding the support points on the other shape along the normal of those planes, and look for the minimum separating axis, by looking for the face / support point whose distance is the "largest". Clear as mud?

Let's go through this in steps, starting with the concept of support points.

Support Function and Support Point

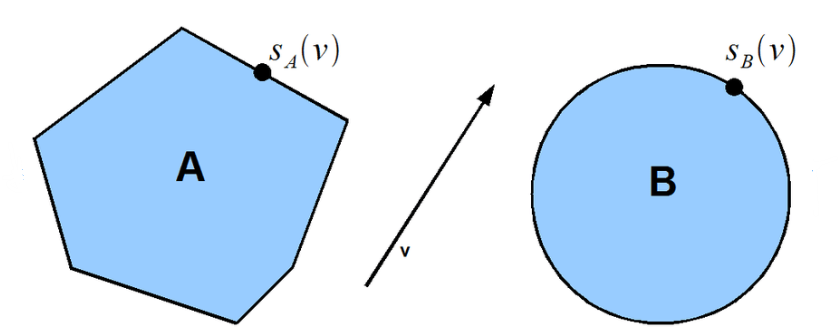
A support function returns a point on the boundary of a shape that is the highest projection on the vector v. The point returned is called the support point. The operation of obtaining the support point is called support mapping.

Geometrically a support point is the farthest point in the shape in the direction of vector v.

For example, the support points of vector v for a polygon A and a circle B are shown below.

Identification of the support point can be done in a variety of ways, but my simple implementation is as follows.

Looking for the minimum penetration axis

Referring to the below picture, assume that the "primary object" is the left one, and the triangle is the "other" object.

It is probably easier to explain the algorithm by looking at the code.

function collide(manifold, bodyA, bodyB)  {
	
	var polyA = bodyA.shape;
	var polyB = bodyB.shape;
	manifold.pointCount = 0;


	let edgeA = 0;
	let separationA = findMaxSeparation(edgeA, polyA, bodyA.xf, polyB, bodyB.xf);
	if (separationA > 0)
		return false;

	let edgeB = 0;
	let separationB = findMaxSeparation(edgeB, polyB, bodyB.xf, polyA, bodyA.xf);
	if (separationB > 0)
		return false;  
	  
	return true;

}

We start by getting the edges of polygon A, loop through the normals, looking for the support points of B in the opposite direction, each time checking the distance of the support point o the relevant face/edge (the distance being measured in the irection of the normal, ie the "signed" distance).

The edge that is associated with the largest distance is the minimum penetration axis.

If this distance is positive, it means that the vertex lies on the positive side of the face normal, ie there is a separating edge and the shapes are not colliding.

We exit early if there is a separating axis.

// Find the max separation between poly1 and poly2 using edge normals from poly1.
function findMaxSeparation(edgeIndex, poly1, xf1, poly2, xf2) {

	var count1 = poly1.count;
	var count2 = poly2.count;
	const n1s = poly1.normals;
	const v1s = poly1.vertices;
	const v2s = poly2.vertices;
	
	var xf = MulT(xf2, xf1);

	let bestIndex = 0;
	let maxSeparation = Number.NEGATIVE_INFINITY;

	for (let i = 0; i < count1; i++) {

		// Get poly1 normal in frame2.
		var n = Rot.MulQV(xf.q, n1s[i]);
		var v1 = Mul(xf, v1s[i]);

		// Find deepest point for normal i.
		let si = Number.MAX_VALUE;
		for (let j = 0; j < count2; ++j) {
			let sij = Dot(n, Vec2.Subtract(v2s[j], v1));
			if (sij < si) {
				si = sij;
			}
		}

		if (si > maxSeparation)		{
			maxSeparation = si;
			bestIndex = i;
		}

	}

	edgeIndex = bestIndex;
	return maxSeparation;

}

Comparison against projection method

In the classic SAT, you project the vertices of both polygons against the face normals of both the polygons. In the support-based SAT, you look for the supoprt point of one polygon against the face normals of the other, and vice versa. So There are fewer checks.

Another difference is that in detecting whether the polygons are colliding, you end up with not only the collision normal and the depth, but also the colliding edge and the colliding vertex, ie:

the translation vector given by the face normal (same as usual SAT algorithm)
the penetration depth given by the distance of the support point to the edge (negative if there is penetration)
vertex with the largest distance (in case of penetration, this would be the "least negative")

With a little bit of additional code you can get the contact point. If you wanted to the more sophisticated clipping method to get contact point(s), you have a slight head-start over the classic SAT because you have the colliding edge information (I'll explore the clipping method in another post).

Application to Circles vs Polygon

Another great thing about this algorithm is that you can apply it to any convex shape if you can write a function to derive the support point for it.

CodePen

You can access a little demo code I've written for this particular version of SAT. It is not particularly elegant nor does it include code for detection of anything other than polygons but hopefully illustrate how this works, much better than my writing!

Sample Code