It's been a while since I finished with my walkthrough of Box2D-Lite.
I thought I would add features that are not available in the original.
I start with an implement of the distance constraint, which is not implemented in Box2D-Lite, but the Jacobian is available in a presentation by Erin Catto here.
What is the distance constraint?
The distance constraint (or distance joint) is a constraint that keeps the distance between two bodies fixed. The bodies are allowed to rotate freely about "anchor points".
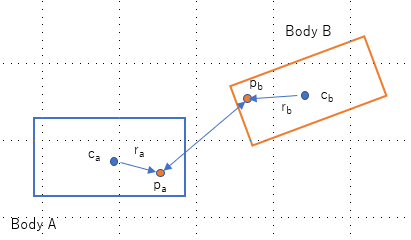
pa, pb = anchor points on body A and body B respectively
ca, cb = center of masses = body.position in world space
ra, rb = vectors pointing from body.position to the anchor point of the respective bodies - this is defined in local space
Applying the Framework
Erin Catto gives the Jacobian as follows:
where d = p2 − p1.
and b2_distance_joint.cpp file of the full version Box2D gives useful guidance notes.
// C = norm(p2 - p1) - L
// u = (p2 - p1) / norm(p2 - p1)
// Cdot = dot(u, v2 + cross(w2, r2) - v1 - cross(w1, r1))
// J = [-u -cross(r1, u) u cross(r2, u)]
// K = J * invM * JT
// = invMass1 + invI1 * cross(r1, u)^2 + invMass2 + invI2 * cross(r2, u)^2
Computing the K-matrix
Again we could go through the entire process of multiplying out the matrices, by noting the similarity with the contact constraint we can say that the K-matrix is:
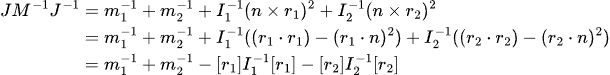
Implementation in Javascript
Knowing the Jacobian and having multiplied out the K-matrix, we can go into the implementation.
The constructor for the Distance class, together with the set function to define the joint is shown below - it is very similar to the Revolute Joint.
class DistanceJoint extends Joint {
constructor() {
super();
this.M = new Mat22();
this.localAnchor1 = new Vec2();
this.localAnchor2 = new Vec2();
this.bias = 0.0;
this.impulseSum = 0.0;
}
set(b1, b2) {
this.body1 = b1;
this.body2 = b2;
var Rot1 = new Mat22(this.body1.rotation);
var Rot2 = new Mat22(this.body2.rotation);
this.localAnchor1 = Vec2.InverseRotateAndTranslate(Rot1, this.body1.position, this.body1.position);
this.localAnchor2 = Vec2.InverseRotateAndTranslate(Rot2, this.body2.position, this.body2.position);
this.length = this.body1.position.to(this.body2.position).length();
this.n = new Vec2();
}
}PreStep
The Prestep function is shown below.
This is also similar to the Revolute function, except the bias is a scalar.
preStep(inv_dt) {
// Pre-compute anchors, mass matrix, and bias.
var Rot1 = new Mat22(this.body1.rotation);
var Rot2 = new Mat22(this.body2.rotation);
this.r1 = Mat22.MultMV(Rot1, this.localAnchor1);
this.r2 = Mat22.MultMV(Rot2, this.localAnchor2);
var p1 = this.body1.position.addi(this.r1);
var p2 = this.body2.position.addi(this.r2);
var dp = p2.subi(p1);
Vec2.Normalize(dp, this.n);
var K = this.body1.invMass + this.body2.invMass
+ this.body1.invI * Vec2.Cross(this.r1, this.n)
+ this.body2.invI * Vec2.Cross(this.r2, this.n)
+ this.gamma;
this.M = 1 / K;
let error = (dp.length() - this.length);
if (world.positionCorrection)
{
this.bias = -this.beta * error * inv_dt;
}
else
{
this.bias = 0;
}
if (world.warmStarting) {
// Apply accumulated impulse.
this.applyImpulse(this.impulseSum);
}
else
{
this.impulseSum = 0;
}
}Solve
Simler than the Revolute method because bias is a scalar.
solve() {
var jv = Joint.getRelativeVelocity(this.body1, this.body2, this.r1, this.r2).dot(this.n);
var lambda = this.M * (this.bias - jv - this.impulseSum * this.gamma);
this.applyImpulse(lambda);
if (world.warmStarting) {
this.impulseSum += lambda;
}
}Derivation of the Jacobian Matrix
Crucial to implementing any constraints is to identify the Jacobian Matrix. Of course I could look it up in any tutorial available on-line, but let us derive it from scratch.
Position constraint function
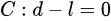
which can be expressed as:
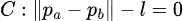
To make things slightly simpler, let's call pa - pb = u, and recalling that the square of the distance between two points is the dot product, we can say that:
Velocity constraint function
now taking the derivative (using the chain rule):
by the chain rule again:
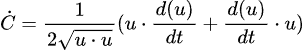
Since the dot product is cumulative and distributive over addition:
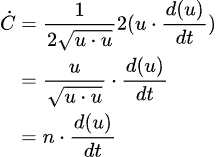
where n is the vector pointing from pb to pa, normalized. The reason for calling this n will become clear, later on.
We know that:
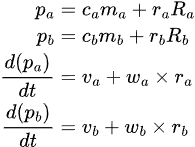
The derivative of a fixed length vector under a rotation frame is the cross product of the angular velocity with that fixed length vector.Therefore:
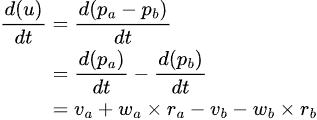
Giving us:
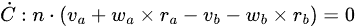
The bit in the rackets is the relative velocity at the "anchor point". This is dotted against the vector pointing from pb to pa, ie the velocity constraint is:
keep the velocity along the vector pointing from the anchor point of body b to anchor point of body a, at zero
In fact, this is very similar to the contact constraint velocity function (it's just that the n is not the collision normal, and it is an equality constraint as opposed to an inequality constraint).
Isolating the velocity
We still need to isolate the velocities to identify the Jacobian. We could go through derivation step-by-step, but noting the similarity with the contact constraint function, we can say that the Jacobian matrix is as follows:
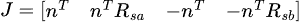
Sample Code
Useful References
Comments