Physics Simulation in Javascript: Circle to Circle Collision Resolution

Resolution of collisions between two circles

In the previous post we discussed how to assess whether two circles are colliding, or penetrating. In this post we talk about how to "resolve" collisions.

What is collision resolution?

As we saw in the circle to wall (axis aligned line) code in the previous post, once collision has been detected, the next step is to "resolve" the collision by moving the objects apart, so that they are "just" touching as opposed to "penetrating". This is necessary since when moving objects around the screen, they can "penetrate" each other - of course in the real world this cannot happen with rigid bodies. However, in the world of computer graphics, it does, and before we get to the interesting part of deciding how the objects behave as a result of the collision, we need to ensure that the objects are "just colliding" as oppose to "penetrating" each other - a process referred to as "collision resolution".

There are various different methods for collision resolution, including the following three:

1. Projection method - simply displace the objects from one another by the depth of penetration. This is simple, but lacks stability when many objects are in close proximity, or resting upon one another, since resolving one penetration can result in a new penetration.

2. Impulse method - use objects' velocities to compute and apply impulses to initiate objects to move in opposite directions. This was made famous by BOX2D

3. Penalty method - this is most complex.

I will go with the Projection method, since it is the simplest to code.

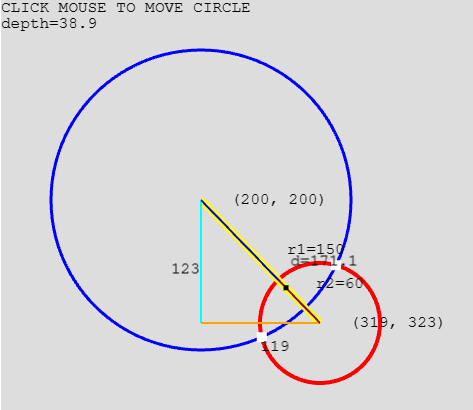
In order to resolve the collision, we need as a minimum the below information (which should be returned in the manifold object):

1. the direction in which to pull the circles apart so they are not touching, and

2. the distance by which the circles must move, or the collision depth.

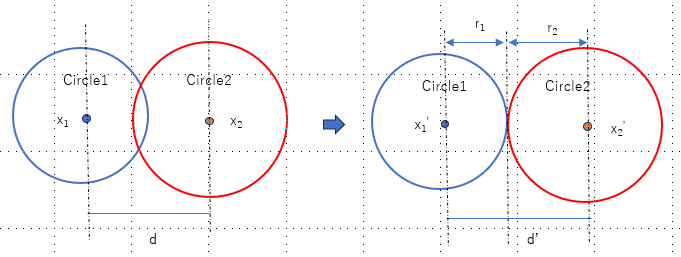
Specifically, what we are trying to do is to move circle A by Δx1 from x1 to x'1 and move circle B by Δx2 from x2 to x'2, such that:

distance(x'1, x'2) = r1 + r2 

or

distance(x'1, x'2) - (r1 + r2) = 0

If we define:

x'1 = x1 + Δx1
x'2 = x2 + Δx2

And define the total amount by which the two circles must move as ∇c, ie:

∇c = Δx1 + Δx2

We know that:

• the magnitude of ∇c is the penetration depth

• the direction is the line joining the 2 centers, ie the collision normal, ie (x1 - x2) / | x1 - x2 |

Where is the "Contact point" or how to "distribute" the resolution?

So we know the direction, and we know the total distance by which the two circles must be pulled apart. We want to move the circles so that they are just "touching" - this is the "contact point". However, how do we determine Δx1 and Δx2, ie how much to move one circle and how much to move the other? ie to distribute the penetration depth?

There are different ways of doing this.

Move by equal amounts

The simplest way is to move the two circles by equal amounts, ie collision.depth / 2.

This is perfectly fine, particularly for circles of equal radii where their movements are not constrained in anyway.

Move proportionally by the respective radii

If you want to take account of the different radii, you can "pro-rate" according to the respective sizes, as follows. The formula is essentially the average of the center points "weighted" by the respective radii. This is also nice and simple and is perfectly fine as long as the movements of both the circles are not constrained (which is the assumption for now).

Move by their inverse masses

At first this may not make little sense. But imagine 2 objects colliding and bouncing part in real life. You would expect the heavier object to bounce off with a smaller velocity (ie move slower) than the lighter object.

I know we are mixing up velocities and positions but we can extend this idea to separating the positions, which is what I have done.

If we define

inverse mass of circle A = w1 = 1 / m1
inverse mass of circle B = w2 = 1 / m2

then,

With that, we can code the separation method as follows - you must be careful with the plus and minus signs.

    static separate(manifold) {

        const b1 = manifold.b1;
        const b2 = manifold.b2;
    
        const eMass = b1.invMass + b2.invMass;

        let sepFactor = manifold.depth / eMass;

        let b1sep = manifold.normal.clone().scale(sepFactor*b1.invMass);
        let b2sep = manifold.normal.clone().scale(sepFactor*b2.invMass);

        b1.pos.subtract(b1sep);
        b2.pos.add(b2sep)

    }

Tunnelling

Note that so far I have only talked about detecting collisions between circles which are not moving.

Things become a little bit more complicated when the circles are moving. Imagine a case where you have small circles moving very fast. The collision detection is executed once frame refresh based on the status of the "static" status of the circles at the particular point in time. It is theoretically possible that during one refresh, one circle could "shoot past" the other circle, hence the collision detection routine would not detect the fact that the circle "collided" with the other circle in between the last time the collision detection routine was executed and the current situation.

This phenomenon is called tunnelling, and is the risk associated with "discrete collision detection" which ignores what happens between the previous and current steps. There are ways to mitigate or overcome this problem, mainly by:

1. increasing the frequency of collision checks (ie do multiple times in one refresh)

2. continuous collision detection (CCD)

Both approaches introduce additional computational overhead. For now, I will plough ahead with discrete static collision detection.

CodePen

Useful References

https://gamedevelopment.tutsplus.com/tutorials/when-worlds-collide-simulating-circle-circle-collisions--gamedev-769

https://gamedevelopment.tutsplus.com/tutorials/how-to-create-a-custom-2d-physics-engine-the-basics-and-impulse-resolution--gamedev-6331

(The above site is fantastic but has lots of equations which do not display correctly. You can copy the "code" to any online latext equation, such as here)

https://digitalrune.github.io/DigitalRune-Documentation/html/138fc8fe-c536-40e0-af6b-0fb7e8eb9623.htm (this explains continuous collision detection)