Understanding 2D Physics Engines with Phaser 3, Part 18: Collision Response with Rotation
- cedarcantab
- Jun 30, 2022
- 6 min read
Updated: Jun 15, 2023
Rectange to Rectangle Collision Response with Rotation
In a prior post we looked at how to identify the contact point of two colliding capsules and calculate the impulse necessary to induce collision response with rotation. What if we wanted to deal with two oriented rectangles? The basic formula to calculate the necessary impulse does not depend on the shape of the geometries involved. The amendments required are:
how to identify the collision (contact) point
how to calculate the mass moment of inertia
In particular (1) is a tricky subject. There are many ways of obtaining the contact point of two colliding rectangles (or convex polygons). The quality of the contact point affects the quality of the simulation.
I refer to a (one) contact point, but in the case of rectangles, a single contact point may not always be sufficient. In this post though, I will explore how we can generate one contact point, just to illustrate that the collision response code developed in the previous post can be applied to rectangles. In a later post I will delve into algorithms to generate multiple contact points.
Simplest method for generating a single contact point
Key points of this method are:
that there is a (one) collision vertex and a (one) collision edge.
the box associated with the projection axes of the shortest overlap is the incident body, and the other body is the reference body.
the collision vertex lies with the reference body and the collision edge lies with the incident body
during the loop to identify the separating axis, the projection axis is made to point from the incident body to the reference body
in order to get the contact point,
project the reference body onto the collision normal
the vertex associated with the min is the contact point
After the contact point has been generated, need to finally ensure that the MTV is pointed in the desired direction (in our convention, from body 1 to body 2)
Consider the following situation.
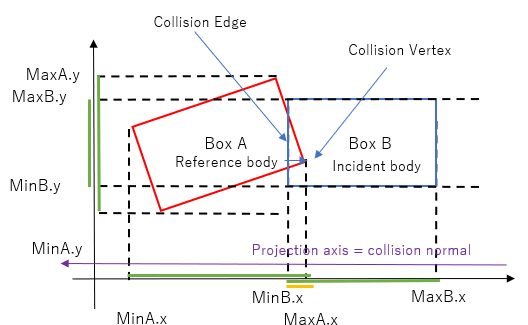
The shortest overlap is between the intervals projected onto the projection axis shown in purple, relating to box B.
The reference body is box A and the incident body is box B. The collision normal is pointing towards the left (as it has been forced to point from the incident body towards the reference body).
Project the reference body onto the collision normal (this is after the shortest overlap has been found). The contact point is the vertex associated with the minimum of the interaval from this projection. You can see why the collision normal must be made to face from the incident body towards the reference body, in order to get the correct vertex.
Now, consider the following situation.
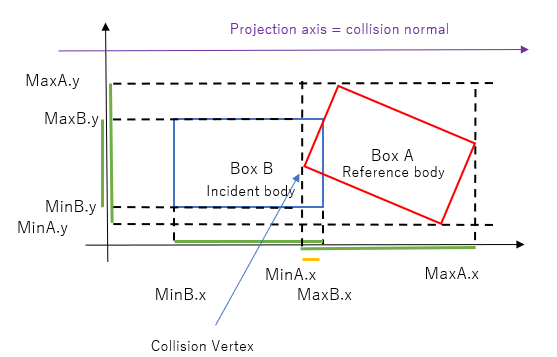
Incident body is box B, and the reference body is box A.
The collision normal has been made to point from the incident body to the reference body. Hence by projecting box A onto this collision normal, the vertex associated with the minimum of the interval is the contact point.
Final check of collision normal direction
Once the collision vertex has been identified, don't forget to finally make sure the collision normal is pointing in the correct direction.
Implementation
But before we get to the implementation of the above, let's do a bit of house cleaning
Interval Class
The Interval class has been amended so that it can hold a vertex, in addition to the min and max information. This is required because of the step of projecting the reference body onto the collision normal, to get the contact point.
class Interval {
constructor(min = Number.MAX_SAFE_INTEGER, max = Number.MIN_SAFE_INTEGER, vertex = new Phaser.Math.Vector2()) {
this.min = min;
this.max = max;
this.vertex = vertex;
}Amended projectVertices method
As mentioned above, there is a step to project the reference body and get the vertex associated with the min of the projection. The projectVertices method has been amended as follows.
projectVertices(axis) {
// this method returns:
// (i) the min and max of the interval, AND
// (ii) the vertex that relates to the min projection
let out = new Interval();
for (let j = 0; j < this.points.length; j++) {
const p = this.dot(this.points[j], axis);
if (p > out.max) {
out.max = p;
}
if (p < out.min) {
out.min = p;
out.vertex.set(this.points[j].x,this.points[j].y);
}
}
return out;
}SAT code
The bulk of the SAT is the same as the code described in the Convex Polygon Collision Detection article. The changes are to:
keep track of the reference body (the body that is NOT the one with the projection axes),
forcing the collision normal to point from the incident body to the reference body
class SAT {
/************************************************************* */
// collision vertex lies with the reference body
// the collision edge lies with the incident body
/************************************************************* */
static detect(bodyA, bodyB, manifold) {
let refObject = null;
let axes1 = boxA.getAxes();
for (let i = 0; i < axes1.length; i++) {
const axis = axes1[i];
const intervalA = boxA.projectVertices(axis);
const intervalB = boxB.projectVertices(axis);
let o = intervalA.getOverlap(intervalB)
if (o < 0) {
return false
}
if (o < manifold.depth) {
// projection axes are from Box A - the reference object is the other object, ie Box B
refObject = boxB;
manifold.depth = o;
manifold.normal = axis;
if (intervalA.max > intervalB.max) {
// negate the normal so that it points from Box A to Box B
manifold.normal.negate();
}
}
};And of course, same amendments made to the second loop.
let axes2 = boxB.getAxes();
for (let i = 0; i < axes2.length; i++) {
const axis = axes2[i]
const intervalA = boxA.projectVertices(axis);
const intervalB = boxB.projectVertices(axis);
let o = intervalA.getOverlap(intervalB)
if (o < 0) {
return false
}
if (o < manifold.depth) {
// projection axes are from Box B - the reference object is the other object, ie Box A
manifold.depth = o;
manifold.normal = axis;
refObject = boxA;
if (intervalA.max < intervalB.max) {
// negate the normal so that it points from Box B to Box A
manifold.normal.negate();
}
}
}Then get the contact point by projecting the reference body onto the collision normal (which at this point is facing from the incident body to the reference body).
// if the shortest overlap is along the Box A axes, the colliding vertex is Box B = refObject
// if the shortest overlap is along the Box B axes, the colliding vertex is Box A = refObject
// at this point the collision normal is facing from the incident object to the refObject
// by projecting the refObject onto this collision normal,
// the vertex associated with the minimum of the interval is the contact point
manifold.cp = refObject.projectVertices(manifold.normal).vertex;Finally make sure that the MTV (collision normal) is facing in the desired direction for use in collision separation / response. After the main loop (before this final check), the normal is pointing from the incident body to the reference body, which may be either of the bodies. Our convention is that the collision normal is pointing from box B to box A. Hence, if the reference body is box A, we are ok. If not, we need to reverse the collision normal.
// finally make sure that the normal is pointing from box B to box A
if (refObject === boxB) {
manifold.normal.negate();
}
MMOI of Rectangle
We have already delved into how to calculate the mmoi of a rectangle in a prior post.
this.density = 0.01; // arbitrary number to multiply to the area to get a nominal "mass" for this 2D object
this.mass = this.width * this.height * this.density;
this.inverse_mass = (this.mass === 0) ? 0 : 1 / this.mass;
this.inertia = (this.mass * (this.height ** 2 + (this.width + 2 * this.height) ** 2)) / 12;
this.inv_inertia = (this.mass === 0) ? 0 : 1 / this.inertia;
Collision response
The algorithm is exactly the same. However, I have restructured the code to make it a bit more easy to maintain, by adding the following 2 methods to the Box class
applyImpulse
getLinearVelocity
applyImpulse(impulse, r) {
this.velocity.add(impulse.clone().scale(this.inverse_mass));
this.angularVelocity += this.inv_inertia * r.cross(impulse);
}
getLinearVelocity(r) {
// return the linear velocity at the point (the arm to the contact point is given)
let omega1 = new Vector2(-this.angularVelocity * r.y, this.angularVelocity * r.x);
return this.velocity.clone().add(omega1);
}
With these 2 methods the method to calculate the collision response impulse now becomes like below:
collisionResponse() {
const normal = this.normal.clone();
const bodyA = this.bodyA;
const bodyB = this.bodyB;
// calculate the "arm" from the center of mass to the contact point
let r1 = new Vector2(this.cp.x - bodyA.position.x, this.cp.y - bodyA.position.y);
let r2 = new Vector2(this.cp.x - bodyB.position.x, this.cp.y - bodyB.position.y);
let r1CrossN = r1.cross(normal);
let r2CrossN = r2.cross(normal);
// calculate the effective mass
let K =
bodyA.inverse_mass + bodyB.inverse_mass +
r1CrossN * r1CrossN * bodyA.inv_inertia +
r2CrossN * r2CrossN * bodyB.inv_inertia;
// calculate relative velocity
let v1 = bodyA.getLinearVelocity(r1);
let v2 = bodyB.getLinearVelocity(r2);
let rv = v1.clone().subtract(v2);
let rvn = rv.dot(normal);
// in case e is different for the two bodies take the smaller of the two
let e = Math.min(bodyA.elasticity, bodyB.elasticity);
// Calculate impulse
let j = -(1 + e) * rvn / K;
let impulse = normal.scale(j);
// apply the calculated impulse to both bodies
bodyA.applyImpulse(impulse, r1);
bodyB.applyImpulse(impulse.negate(), r2)
}

Comments