Physics Simulation in Javascript: Circle2Circle Collision Response (Bounce)
- cedarcantab
- Feb 15, 2022
- 5 min read
Updated: Jun 17, 2023
Circle vs Circle Collision Response
In the previous post I covered:
detecting collisions (strictly speaking, overlap) between two circles, and
resolving the collision of two circles using the Projection Method, which allowed you to "push" circles around the screen.
As outlined in the previous post, collision resolution using the projection method is the act of directly changing the position of the overlapping objects so that they no longer overlap. It does not change the velocity (or acceleration) of the objects, hence after the collision resolution, the objects will continue to try & move in the direction that they were travelling in, prior to the collision - more likely than not, this will mean that the objects will end up overlapping again. In the "real" world, when two objects collide, you would expect the bodies to "respond" in some way, typically bounce away from each other. This is what "collision response" is all about.

Introduction
In essence collision response is about:
applying impulse to change the velocity along the collision normal to effect "bounce"
applying impulse to change the velocity along the collision tangent to simulate friction.
Before we get into the maths, we will talk briefly about the following key concepts:
change in velocity, Δv
impulse
decomposition of velocity and impulse
relative velocity
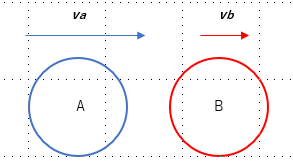
Consider the following situation of two balls - ball A and ball B - colliding.
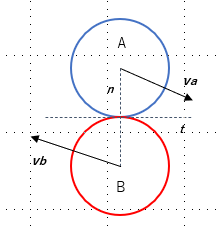
where:
Ball A has mass m(a) and is moving with velocity v(a)
Ball B has mass m(b) and is moving with velocity v(b)
n is the collision normal (unit size), which is pointing in the same direction as v (it is critical to be aware of the direction of the collision normal - otherwise the formula will not give you the correct result)
t is the unit vector perpendicular to the collision normal
We are looking for Δv to calculate post-collision velocities
We are wanting calculate the velocities of the balls post collision - call that v'(a) and v'(b), one can say that we want to calculate the change in velocities Δv(a) and Δv(b) such that:
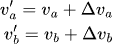
Impulse = change in momentum
Impulse can be thought of as the change in momentum (momentum being velocity x mass). I don't know why, but in the context of physics engines, capital letter J is typically used to denote the impulse.
J = mv' - mv = mΔv
where:
v is the pre-collision velocity
v' is the post-collision velocity
This may be expressed as:
v' = v + Δv = v + J / m
ie the change in velocity from pre- to post- collision = J / mIf you look at the above, you can see that what the equation is telling us that the change in velocity (Δv = J / m) is inversely proportional to the mass - which makes intuitive sense.
Assume impulse J is applied to a pair of balls
Now consider the two colliding balls as a "system" and assume an impulse J is applied to this system.
We can say the following (note the signs in these equations - this assumes that the collision normal and J are both pointing from A to B).
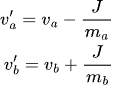
subtracting these equations gives:
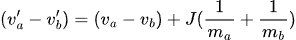
Relative Velocity
As explained in this site here, if you have objects a and b moving with velocities Va and Vb, the velocity of object a relative to the object b is expressed as below. It is vital that we are aware of the 'direction' of this relative velocity vector. Whereas the below definition subtracts the velocity of object b from that of object a, some implementations or tutorials will define it the other way around, i.e. subtract velocity of object a from that of object b.
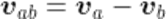
Consider the below situation where two balls are moving horizontally in the same direction but ball A is moving at a much faster speed than B. So A will catch-up and collide with B at some later time. If you calculate v(ab) as per above, it will yield a vector that is pointing in the positive x-direction, whereas calculating it the other way around will yield a relative velocity vector pointing towards the 'left', ie the negative x-axis.
Intuitively, you can imagine that in the above situation will result A slowing down and B speeding up after the collision.
Combining this with set of equations from the impulse section, we can say that:

Decomposition into components along the collision normal and collision tangent
We can decompose a given velocity (indeed any vector) into components along the collision normal and collision tangent as follows:
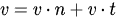
Similarly, we can decompose impulse J as follows:
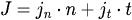
where:
jn is the magnitude of the component of J along the collision normal
jt is the magnitude of the component of J along the collision tangent
The Impulse Method
When two bodies collide we can apply an impulse between them to change their velocity. For a frictionless bodies, the direction of the impulse will be in the normal direction.
Calculating the impulse
The important part is knowing the necessary impulse or J to get post-collision behaviour right.
Normal component of J
Let's try to figure out the normal component of impulse J first, ie the impulse to effect bounce.
We know that:

As a first step, perform the dot product with the n vector on both sides (remember that dot product between two perpendicular vectors is zero - it n dot t = 0).
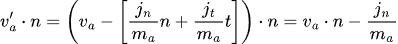
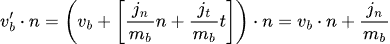
Subtracting the preceding two equations results in the following:

Given how we have defined relative velocity the above equation simplifies to:
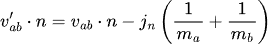
If we assume that:
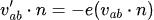
where e = coefficient of restitution (If e = 1, the body is perfectly elastic the relevative velocity along the normal just flips sign, retaining the same speed. If e = 0, the body is perfectly inelastic and the velocity along the normal is "killed off").
Given the above, we can say that:

Collecting the terms and solving for j(n), the impulse in the normal direction result in the following:

Implementation
Collision Detection
As a reminder, the code to detect collision is as follows
class CircleDetector {
static detect(b1, b2, manifold) {
var v = new Vec2(b2.pos.x - b1.pos.x, b2.pos.y - b1.pos.y);
// note v is pointing from b1 to b2;
var mag = v.lengthSq();
const radii = b1.shape.radius + b2.shape.radius;
if (mag < radii * radii) {
// then we have a collision
manifold.depth = radii - v.length();
v.normalize();
manifold.normal.copy(v);
return true;
}
return false;
}
}
Note the direction of the collision normal. It is pointing from circle A to circle B - you need to aware of the "direction" of both the relative velocity and the collision normal in applying all of this theory correctly.
Once collision has been detected by the above, the collision manifold is passed to the following two methods, together with the two circle objects for collision resolution and response.
Resolving the collision
We resolve the collision, or separate the overlapping circles, with the projection method, ie directly shifting the positions of the circles.
static separate(manifold) {
const b1 = manifold.b1;
const b2 = manifold.b2;
const eMass = b1.invMass + b2.invMass;
let sepFactor = manifold.depth / eMass;
let b1sep = manifold.normal.clone().scale(sepFactor*b1.invMass);
let b2sep = manifold.normal.clone().scale(sepFactor*b2.invMass);
b1.pos.subtract(b1sep);
b2.pos.add(b2sep)
}Collision Response
And below is the main topic of this post - the code to calculate the collision response.
We can implement the above very easily, given that we have the normal vector and the pre-collision velocities of the two circles.
I have only implemented the impulse along the normal and ignored the component along the tangent, although it would be easy addition.
static response(manifold) {
const b1 = manifold.b1;
const b2 = manifold.b2;
const eMass = b1.invMass + b2.invMass;
// calculate the relative velocity
let rv = new Vec2(b1.velocity.x - b2.velocity.x, b1.velocity.y - b2.velocity.y);
// project the relative velocity onto the normal
let rvn = rv.dot(manifold.normal); // relative velocity vector projected onto the collision normal vector
let e = Math.min(b1.e, b2.e);
let j = (1 + e) * rvn / eMass;
let impulse = manifold.normal.clone().scale(j);
b1.velocity.subtract(impulse.clone().scale(b1.invMass));
b2.velocity.add(impulse.clone().scale(b2.invMass));
}Codepen
Useful References
http://www.chrishecker.com/images/e/e7/Gdmphys3.pdf (this has all the information you need for coding basic collision response)
https://research.ncl.ac.uk/game/mastersdegree/gametechnologies/physicstutorials/5collisionresponse/Physics%20-%20Collision%20Response.pdf (this is another great article which gives a more "intuitive" explanation of the impulse method)
https://www.youtube.com/watch?v=1L2g4ZqmFLQ (content if same as paper above but in video)
https://www.youtube.com/results?search_query=science+abc+bouncy (very good video on coefficient of restitution)
(The above site is fantastic but has lots of equations which do not display correctly. You can copy the "code" to any online latext equation, such as here)


Comments