Understanding 2D Physics Engines with Phaser 3, Part 21: Local (Model) space vs World space

Local vs World space

In this post I document the introduction of the concept of local space vs world space.

Frankly, the concepts are not so easily explained in words, and more easily understood by looking at the code, so this post is a bit short.

The Body class in Local (Model) Space

There are several reasons for creating a separate Body class, the main one being to introduce the concept of local vs world space.

The body's position will be defined with reference to the world space. It will have the position in terms of (x,y) and angle of rotation. It is useful to think of the body as a "point". The "shape" of the body will be defined separately from the body with reference to its own local space. The shape will be "attached" to the body.

World space is the position of the body in the "overall space" in all my demos so far, the world space was the "screen" as defined by width and height in the config object when the game scene was initiated (typically, I have chosen 600 x 600).

That was all have used to date.

Now we introduce the concept of local space

Local space is difficult concept to explain in words. It is the frame of reference to local to the shape. Each shape will have its own "local space", and its vertices will be defined with reference to this local space. In practical terms, the vertices of a shape is defined with reference to (0,0) in the local space. It is useful to have the center of mass of the shape positioned at (0,0) in local space. So a box with width of 100 and height of 50 will have its vertices at:

Vertex 1: (-50,-25),
Vertex 2: (50,-25),
Vertex 3: (50,25), and
Vertex 4: (-50,25).

When the shape is drawn in world space, the vertices are "transformed" to world space, which is defined for the body that the shape is attached to. So, if the above rectangle shape is attached to a body that is positioned at (70,50) with no rotation, the rectangle's vertices in world space will be transformed as follows:

Vertex 1: (-50,-25) => (-50+70=20, -25+50=25)
Vertex 2: (50,-25) => (50+70=120, -25+50=25)
Vertex 3: (50,25) => (50+70=120, 25+50=75)
Vertex 4: (-50,25) => (-50+70=20, 25+50=75)

Transforming from one frame of reference to another

In the above example, the transformation from local space to world space was just a matter of adding the world space x and y positions to the local space coordinates of the vertices of the shape. This transformation is called translation.

What if the body was rotated? We have looked at how a point can be rotated around the origin by multiplying the point by a rotation matrix. To transform vertices of a body to world space when the body is rotated, the vertices will need to be rotated, then translated. The order is important.

This type of transformation (sometimes referred to as affine transformation) can be achieved by means of multiplying the vertex local coordinates by an augmented matrix which combines a rotation matrix and translation transformation into one matrix, like so:

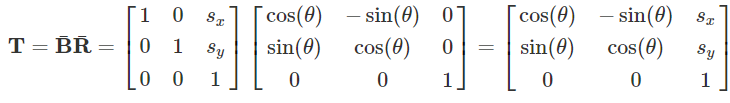
Moving to one frame of reference to another

In physics simulations there is a need to constantly move from local to world space and vice versa. We have already covered how to do this, when I touched on Phaser's transform matrix. I also noted in the same post that transformation matrix class was a bit sparse on methods. Hence, I have relied on a transform class, that is based on the Dyn4j physics engine.

When implementing you need to be very aware which frame of reference you working in, but once its implemented, it does make things easier.

In fact, in certain cases it makes the code considerably easier by choosing the right frame of reference.

For example, imagine you are wanting to bounce a ball off an uneven terrain. We have already covered collision detection of circle against a line segment using the separating axis theorem. However, by transforming the ball's position into the line segment's local space, the collision detection becomes that of collision detection against axis aligned line segment.

First create a simple body class that contains the basic properties for a physics "point". To the constructor is fed (x,y) which is the position of the body in world space, and angle which is the orientation of the body also in world space.

class Body {
  constructor(scene, x, y, angle = 0) {
    this.scene = scene;
    this.graphics = scene.graphics;
    
    this.position = new Phaser.Math.Vector2(x,y);
    this.velocity = new Phaser.Math.Vector2(); // give it a bit of sideways velocity
    this.angle = angle;
    
    this.u = new Transform();
    this.u.applyITRS(this.position.x, this.position.y, this.angle, 1, 1); 
    
    this.restitution = 0;
  }

  update(dt) {
    this.velocity.add(this.scene.gravity.clone().scale(dt));
    this.position.add(this.velocity.clone().scale(dt))
  }
 
}

A Ball class can then extend the Body class (you could also "add" this geometry to the body class as a property).

class Ball extends Body {
  constructor(scene, x, y, r ) {
    super (scene, x, y);
    this.radius = r;
     
  }

The line segment class can be constructed as follows. The "ends" of the line segment are fed to the Segment Class constructor in world space coordinates. The mid-point and the orientation of the line segment are calculated and fed to the Body class. In addition, the "ends" of the line segment are converted into local space and stored as this.v1 and this.v2.

class Segment extends Body {
 
  constructor(scene, x1, y1, x2, y2) {
    
    super(scene, (x1+x2)/2, (y1+y2)/2,  Math.atan2(y2 - y1, x2 - x1))  

    this.len = Math.sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
    this.v1 = new Phaser.Math.Vector2(-this.len/2, 0);
    this.v2 = new Phaser.Math.Vector2(this.len/2, 0);
  
  }

Detect intersection in line segment's local space

Ans here is the clever bit. The code (within the ball class) to detect intersection of the circle against a line segment is shown below.

 ballToGround(g) { // g is the line segment to be tested against
 
    // transform ball's position into ground local space
    var tpos = new Phaser.Math.Vector2(); // tpos to hold transformed ball position
    g.u.applyInverse(this.position.x, this.position.y, tpos); // apply the inverse of the ground's world matrix to ball's position, ie map ball's world position to ground's local space 
    // transorm ball's velocity angle to ground local angle
    var tvel = new Phaser.Math.Vector2(); // tvel to hold transformed ball velocity
    g.u.applyInverseRotation(this.velocity.x, this.velocity.y, tvel); // for velocity, only need to map it's rotation to ground local space - ignore translation

    // once transformed into ground local space, collision checking is against axis aligned space
    
    if (tpos.x >= g.v1.x && tpos.x < g.v2.x  && // ball horizontal position is "within" the ground segment
        tpos.y + this.radius > 0 ) // the bottom of the ball is "below" the ground      
    {
      tpos.y = -this.radius; // position correction
      tvel.y *= -this.restitution;
    }
    
    // transform ball's position back to original ball (world) space
    g.u.transformPoint(tpos.x, tpos.y, this.position);
    // rotate ball's velocity to original ball space
    g.u.applyRotation(tvel.x, tvel.y, this.velocity)

  }