Physics Simulation in Javascript: Circle to Circle Collision Detection

Collision Detection and Collision Resolution between 2 Circles

One of the core functions of a physics engine is of course to detect when objects have collided, ie carry out collision detection. Only when you have detected collision, can you get information about the nature of the collision and then decide the post-collision behavior of the objects.

The simpler an item's shape, the fewer computations are required to determine if it has collided with another object. In the previous post I created the one of the simplest of collision detections, namely collisions between circles and a "line", and importantly, the "lines" were along the x and y axis (axis aligned).

In this post, I will look at the next most simple of all collision detections - that between two circles.

Collision detection between 2 circles

In principle, the algorithm to detect whether two circles intersect is quite straightforward. If the distance between the centers of the two circles is less than the sum of the radii of the two circles, then an intersection has occurred.

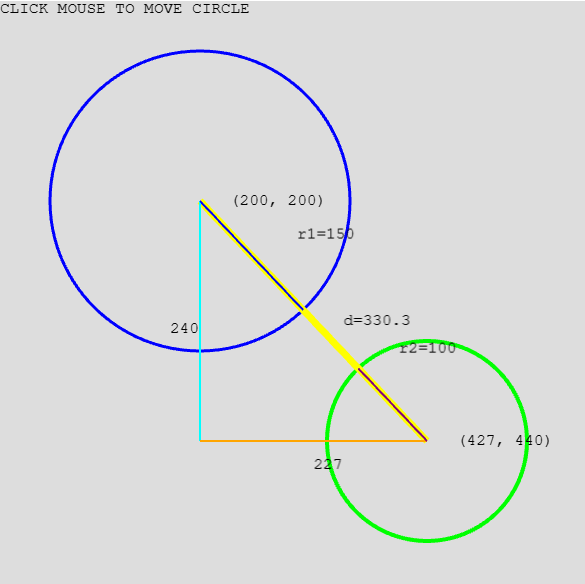
We know the radii of the respective circles (since we define them), but how do we calculate the distance between the center points? We can apply the Pythagoras' theorem to the triangle formed by points centers of the two circles and the "imaginary" (blueCircle.x, greenCircle.y).

Detecting overlap formula

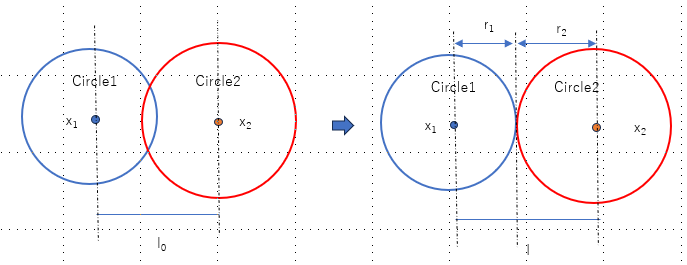
So, once we know the distance between the centers, we can compare that to the sum of the radii. If the distance d is less than the sum of the radii, then we know that the circles "overlap" or colliding, ie:

var overlap = (distance(x1, x2) < (r1 + r2))

Depth of overlap and Collision normal

Detecting whether two circles overlap is easy. However, in the real world, shapes do not overlap. In computer physics simluations, once an overlap has been detected, that overlap must be "resolved" (ie the "unreal" overlap situation needs to be fixed) by moving the circles apart so that they are just colliding, ie just touching.

In order to do this, we need to know:

1. depth of overlap (or depth of penetration): how much to move the two circles apart, and

2. collision normal: in which direct to move the circles

Depth of penetration

The depth of peentration is easy enough to find - it is the difference between the sum of the radii and the actual distance between the two centers.

We know that there is overlap if distance(x1, x2) < sum of radii.

It should also be intuitively obvious that:

depth of overlap = sum of radii - distance(x1, x2)

The output from the formula above will be positive if there is overlap and negative if there is separation.

Collision normal

It should also be intuitively obvious that the circles can be most efficiently separated by moving them apart along the line that joins the 2 centers.

In general, this "direction" in which the shape can be moved by the least amount to make them separate is called the collision normal (this concept is very important in physics simulations of colliding bodies).

collision normal = circleA.center - circleB.center

Collision tangent

As an aside, the "vector" perpendicular to the collision normal is referred to as the collision tangent. This is also an important oncept as it will be needed for things like simulation of friction.

Collision Manifold

In order to manipulate the circles after a contact has been detected requires us to keep hold various information describing the nature of the overlap, such as below (not all of these will be used for our simple demo right now):

1. penetration depth,

2. collision normal,

3. collision tangent,

4. colliding vertex, colliding edge

It is convenient to hold such properties in an object called the collision manifold, like below.

class Manifold {

  constructor(b1, b2) {
	
	this.b1 = b1;
	this.b2 = b2;

	this.depth;
	this.normal = new Vec2();
	this.e = null; // edge
	this.v = null; // vertex 
  
  }	

}

Code to detect Overlap

And finally the actual code to detect overlap between two circles.

class CircleDetector {

	static detect(b1, b2, manifold) {

		var v = new Vec2(b2.pos.x - b1.pos.x, b2.pos.y - b1.pos.y);
		// note v is pointing from b1 to b2;
		var mag = v.lengthSq();
		const radii = b1.shape.radius + b2.shape.radius;

		if (mag < radii * radii) {
			// then we have a collision
			manifold.depth = radii - v.length();
			v.normalize();
			manifold.normal.copy(v);
			return true;
		}

		return false;

	}

}

This method will tell us whether the two circles overlap not, and if they are overlapping, return various collision information in the manifold object.

The information returned in the manifold can be used to separate the circles, which is the subject of the next post.