Understanding 2D Physics Engines with Phaser 3, Part 11.1: SAT - Convex Polygon Collision Detection
- cedarcantab
- Mar 23, 2022
- 6 min read
Updated: May 11, 2023
Collision Detection between Polygons with Separating Axis Theorem

Phaser provides methods to detect overlap / collision between triangles and rectangles (see post here).
The algorithm for triangle intersection Geom.Intersects.TriangleToTriangle is based on checking every edge of one triangle against every edge of the other triangle for intersections, and then finally checking whether the one of the triangles was entirely contained within the other. The Geom.Intersects.RectangleToRectangle is - which only works for axis aligned rectangles - is easier. It looks to see if any of the parallel edges "overlap".
As discussed in a prior post, Phaser does not provide a generic polygon version of such methods.
In this post, I look at something called the Separating Axis Theorem (SAT), which is a popular method for detecting collisions between convex polygons (note the polygon intersection algorithms presented in the prior post can detect intersections between concave polygons. However the algorithms are computationally expensive).
Note, my example code has been created with ease of understanding in mind (for myself) and is not the most efficient way of implementing SAT.
The basic thinking behind SAT
There are lots of articles out there but for those wanting to implement it in code (I personally found this one to be the easiest to understand), but in summary:
The Separating Axis Theorem (SAT for short) states if you are able to draw a line to separate two polygons, then they do not collide.
This is stating the obvious. All it is saying is that if you can draw a line that separates the polygons, the polygons are...separated.
However, the question is, how do you assess this? You can see from below diagram that you can draw infinite number of lines that separate two polygons - you cannot loop through all possible separating lines!

Conceptually, SAT identifies a separating line by looking for existence of overlap between the intervals resulting from projecting the polygons onto a limited number of projection axes. The below diagram shows that the intervals in green that are the result of projecting the polygons on to the projection axis. The intervals do not overlap. This means that there is a separating line, ie the polygons do not overlap. (When there is a separating line, the projection axis is called the separating axis).

The clever part of SAT is that, you only need to do this projection / interval overlap test for a limited set of projection axes. These projection axes are the normals of the edges of the respective polygons.
In fact, once you understand the above, you will appreciate the sheer elegance of this theory. This site here explains the idea of projections and how to determine whether the projections overlap or not, using lots of diagrams.
New Polygon Class class
To experiment with this algorithm, I have created a new polygon class by extending Phaser's Geom.Polygon class.
My version takes the x, y coordinate (the "center"), the "radius" and the number of vertices, to create a regular polygon. It's a bit crude, but below is the beginning of the constructor function of this class.
The vertices are created in clockwise order, in the Phaser's screen coordinate system of x-axis pointing right and y-axis pointing downwards. Knowing the order is important when it comes to collision separation - not strictly relevant for collision detection).
class Polygon extends Phaser.Geom.Polygon {
constructor(scene, x, y, r, vertices) {
super();
this.scene = scene;
this.type = "polygon";
let tmpArray = [];
for (let i = 0; i<vertices; i++)
{
tmpArray.push(x+Math.cos(i*2*Math.PI/vertices)*r, y+Math.sin(i*2*Math.PI/vertices)*r)
}
this.setTo(tmpArray);Having got that out of the way, let's delve into the implementation of SAT.
Key components
In terms of implementation, there are several key elements to the SAT test.
identifying the projection axes
projecting the vertices on the projection axes and identifying the interval from the projections
assessing whether the intervals overlap
We will go through these elements in turn.
Identifying the projection axes
I have created a method called getAxes in the above Polygon class to return the projection axes.
The logic is simple. Loop through all the edges and create the orthogonal vector for each using the normalizeLetHand method (this creates vectors that are facing outward, as opposed to inward).
Which way the projection axes are pointed is not strictly relevant for collision detection. However, it will become critical to be consistent when it comes to collision separation.
getAxes() {
var axes = [];
for (let i = 0; i < this.points.length; i++)
{
const va = this.points[i];
const vb = this.points[(i+1) % this.points.length];
// obtain projection axis by rotating the edge to its perpendicular and normalising it
const axis = new Phaser.Math.Vector2(vb.x-va.x, vb.y-va.y).normalizeLeftHand().normalize();
axes.push(axis);
}
return axes;
}Projecting all the vertices to obtain the 'maximum' and 'minimum'
For Step 3, we need a method which projects all the vertices onto the given projection axis, and returns the minimum and maximum projected values. The "gap" between the minimum and maximum is the "interval".
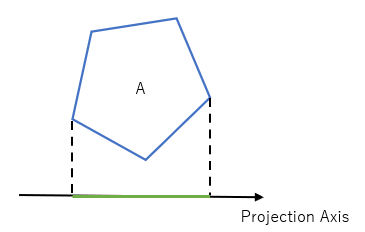
Within the Polygon class, the following method has been created to loop through all the vertices, project them onto the given axis, get the maximum and minimum and storing them in a custom Interval object.
projectVertices(axis) {
let out = new Interval();
for (let j = 0; j < this.points.length; j++)
{
const p = this.dot(this.points[j], axis);
if (p > out.max)
{
out.max = p;
}
if (p < out.min)
{
out.min = p;
out.vertex.set(this.points[j].x,this.points[j].y);
}
}
return out;
}The interval object, which is a class that contains the min and max values of an interval, together with some useful methods, is as below.
class Interval {
constructor(min = Number.MAX_SAFE_INTEGER, max = Number.MIN_SAFE_INTEGER, vertex = new Phaser.Math.Vector2()) {
this.min = min;
this.max = max;
this.vertex = vertex;
}
Assessing overlap of intervals
Having obtained the interval from the above, how do we assess whether these are overlapping or not?
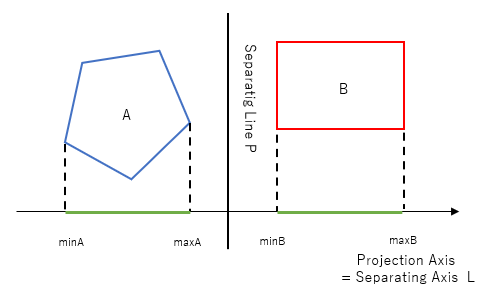
We have seen this test before in the axis-aligned rectangle intersection test.
One can see from the diagram above that the green line segments are separated (ie NOT overlapping) if:
minB > maxA (ie the left edge of the interval on the right is to the right of the right edge of the left interval, as in the diagram), OR
minA > maxB (the opposite of the above)
There is another way, which is to calculate the amount of "overlap" of the intervals. This may be done with the following formula:
Math.min(maxA, maxB) - Math.max(minA, minB)If you try this formula on the below situation you will get a positive number, indicating the overlap amount.
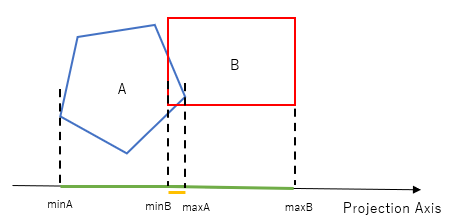
If you apply the formula to the separating case, you will get a negative number.
Having the magnitude of overlap is useful (critical) when we come to implement collision separation and response.
Main detection code
With the above components, it is relatively easy to implement the SAT.
Get the projection axes from PolygonA. For each projection axis, project both the polygons, and check for separation. If there any pair of intervals are separated, it means the polygons are separated.
sat(polygonA, polygonB) {
// get the projection axes from PolygonA
let axes1 = polygonA.getAxes();
// now loop through all the projection axes, and project the polygons onto each
for (let i = 0; i < axes1.length; i++) {
const axis = axes1[i];
// get the extreme points of the vertices as they are projected on the projection axis
const intervalA = polygonA.projectVertices(axis);
//Do the same for each vertex in polygonB:
const intervalB = polygonB.projectVertices(axis);
// if the intervals do not overlap then the two shapes cannot be intersecting
if (!intervalA.overlaps(intervalB)) {
// the shapes cannot be intersecting so immediately return false
return false;
}
} // We have completed all the face normals of Polygon ARepeat the same process but with the projection axes obtained from PolygonB.
// Now get the projection axes from Polygon B and repeat the process
let axes2 = polygonB.getAxes();
for (let i = 0; i < axes2.length; i++) {
const axis = axes2[i]
const intervalA = polygonA.projectVertices(axis);
const intervalB = polygonB.projectVertices(axis);
// if the intervals do not overlap then the two shapes
// cannot be intersecting
if (!intervalA.overlaps(intervalB)) {
// the shapes cannot be intersecting so immediately return null
return false;
}
}
// if we have got to here it means we could not find a separating line so return true
return trueIf we end up working through all of the projection axes from both the polygons without detecting a pair of separated intervals, it means that there is no separating axis, hence the polygons must be colliding.
Sample Code
Useful References
https://dyn4j.org/2010/01/sat/ (I personally found this one to be easiest to understand, and I have based much of my Javascript implementation on the Java version of this site)
https://youtu.be/-EsWKT7Doww (or if you prefer watching video, this is easy to understand)
https://youtu.be/ntszkDJseYQ (very short video but with source code, in C++)
http://programmerart.weebly.com/separating-axis-theorem.html (this has Javascript code)


Comments