Phaser 3 TransformMatrix
In the previous post we looked at how a point can be rotated about the origin through multiplying the position of the point by the rotation matrix (in maths speak, confusingly this is one form of linear transformation).
Shifting a point by a certain distance in a straight line is referred to as translation. If you want to move a point at coordinates (x=50, y=25) by 70 pixels in the x-direction and 40 pixels in the y-direction, then you just need to add the translation vector (70, 40) to the point's coordinates. Translation is, confusingly, a not a linear transformation.
In order to rotate a point around the origin and then translate it, you could perform the following 2 steps in sequence (order is important):
multiply the point's coordinates by the relevant rotation matrix, then
add the relevant translation vector
What if you wanted to do this in "one" operation? In fact you can, through something called affine transformation which is a combination a linear transformation and translation. Basically, by creating something called an affine transformation matrix, you can rotate a point and then translate it, with one matrix multiplication. The affine transformation matrix for rotating a point around the origin by θ and translate by (Sx, Sy) in 2D is as below.
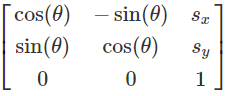
You will note that it is a 3x3 matrix. So how do you multiply a 2D vector by a 3x3 matrix? I will not go into the details as to why, but you simply append a 1 to the end of the 2D vector.
In fact, by creating this one transformation matrix you can carry out the following transformations in one operation.
translate,
rotate,
scale,
reflect, and
skew
But how do we deal with the matrix multiplication?
Phaser actually provides an object and relevant - it is called.. TransformationMatrix
Phaser.GameObjects.Components. TransformMatrix
The official documentation does not go into much detail except to state that this is a matrix used for display transformations for rendering, and is represented lie so:
| a | c | tx |
| b | d | ty |
| 0 | 0 | 1 |
Looking into the code, Phaser holds the individual entries in the above matrix in a one-dimensional array (not in a 2D array) in a property called this.matrix.
this.matrix = new Float32Array([ a, b, c, d, tx, ty, 0, 0, 1 ]);In otherwords,
matrix[0] = a = scale X value
matrix[1] = b = skew Y value
matrix[2] = c = skew X value
matrix[3] = d = scale Y value
matrix[4] = tx = translate X value
matrix[5] = ty= translate Y value
matrix[6] = element in 3rd row, 1st column of transformation matrix = 0
matrix[7] = element in 3rd row, 2nd column of transformation matrix = 0
matrix[8] = element in 3rd row, 3rd column of transformation matrix = 1
Not that it is particularly relevant, but as far as I can tell, none of the methods actually use matrix[6]...matrix[8] as the methods do not use generic n x n matrix multiplication algorithms.
But you do not really need to know this, as Phaser provides you with basic methods necessary to apply transformation to a point. The key methods are:
applyITRS(x, y, rotation, scaleX, scaleY),
transformPoint(x, y, point), and
applyInverse(x, y, [, output])
applyITRS(x, y, rotation, scaleX, scaleY)
The documentation states that this method
Apply the identity, translate, rotate and scale operations on the Matrix.
This is the basic method to set the transformation matrix. More often that not, you would be interested in only rotation and translation - it is critical to remember to pass scaleX=1 and scaleY=1.
var radianSin = Math.sin(rotation);
var radianCos = Math.cos(rotation);
// Translate
matrix[4] = x;
matrix[5] = y;
// Rotate and Scale
matrix[0] = radianCos * scaleX;
matrix[1] = radianSin * scaleX;
matrix[2] = -radianSin * scaleY;
matrix[3] = radianCos * scaleY;transformPoint(x, y, point)
This method transforms point (x,y) by performing the matrix multiplication of point (x,y) and the transformation matrix, and returning the result in an object with x and y properties (a Vector2 like object).
transformPoint: function (x, y, point)
{
if (point === undefined) { point = { x: 0, y: 0 }; }
var matrix = this.matrix;
var a = matrix[0];
var b = matrix[1];
var c = matrix[2];
var d = matrix[3];
var tx = matrix[4];
var ty = matrix[5];
point.x = x * a + y * c + tx;
point.y = x * b + y * d + ty;
return point;
},applyInverse(x, y [, output])
I have not covered the concept of local vs world space yet. For now just for let us note that transformPoint(x,y, point) is typically used to transform from local to world space, but quite often it is necessary to move from world to local space, in which case this method can be used.
You may remember from school that an inverse of a 2x2 matrix A:
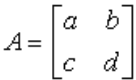
is
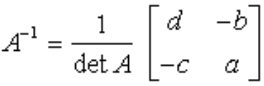
where det A is the determinant of A, defined as (a*d-b*c)
Looking at the underlying code, this method is applying the above formula to the point, without actually changing the original transformation matrix
var id = 1 / ((a * d) + (c * -b));
output.x = (d * id * x) + (-c * id * y) + (((ty * c) - (tx * d)) * id);
output.y = (a * id * y) + (-b * id * x) + (((-ty * a) + (tx * b)) * id);
Other useful methods
You can go a very long way with just the above three methods, but I have found below methods also useful on occasions.
invert()
Inverts the existing transformation matrix. Looking at the underlying code, this method is using the 2x2 matrix inversion formula, changing the original matrix elements.
var n = a * d - b * c;
matrix[0] = d / n;
matrix[1] = -b / n;
matrix[2] = -c / n;
matrix[3] = a / n;
matrix[4] = (c * ty - d * tx) / n;
matrix[5] = -(a * ty - b * tx) / n;
return this;multiply(rhs [, out])
Official documentation states:
Multiply this Matrix by the given Matrix.
Both the rhs matrix and the out matrix are in the TransformMatrix format.
This is performing a 3x3 matrix optimized to take into account the 0's and 1's.
var destinationMatrix = (out === undefined) ? this : out;
destinationMatrix.a = (sourceA * localA) + (sourceB * localC);
destinationMatrix.b = (sourceA * localB) + (sourceB * localD);
destinationMatrix.c = (sourceC * localA) + (sourceD * localC);
destinationMatrix.d = (sourceC * localB) + (sourceD * localD);
destinationMatrix.e = (sourceE * localA) + (sourceF * localC) + localE;
destinationMatrix.f = (sourceE * localB) + (sourceF * localD) + localF;
return destinationMatrix;
Useful References
Comments