There is one special type of matrix that will come up time and time again, particularly we start to deal with rotating bodies; that is the rotation matrix. It is useful to delve further into this particular type of matrix.
The Rotation Matrix
A rotation matrix is defined as follows.
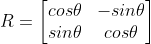
This matrix will rotate a vector v by means of the following matrix multiplication.
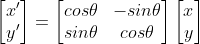
In fact, the below Wiki page explains the concept of 2D rotations very well (and goes onto explain 3D).
In a nut-shell, you can rotate a point counterclockwise through an angle θ about the origin in a right-handed 2D Cartesian coordinate system by multiplying the point expressed as vector v, by the rotation matrix R, as below.
And that really is it.
In terms of practicalities, the following are important to note:
The above rotation matrix describe rotations about the origin
The rotation matrix rotates a point by an incremental angle of θ. It does not rotate the point to absolute angle of θ
The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. −90°).
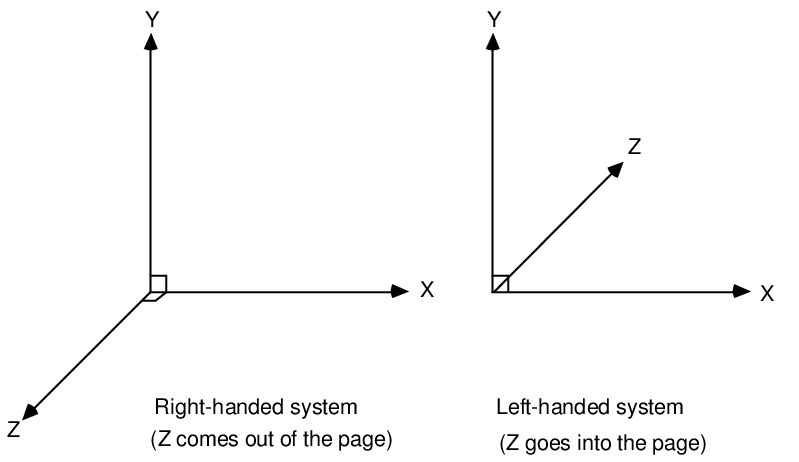
You need to be aware of the coordinate system.
Put simply, textbook explanations will assume the "standard" coordinate system of x-coordinate pointing to the right, and the y-axis pointing upwards, or y counterclockwise from x. This is called the right-handed coordinate system (see below for explanation of this).
The Javascript screen coordinate system (and most computer displays does not work this way. As Wiki explains, if a left-handed Cartesian coordinate system is used, with x directed to the right but y directed down, R(θ) is clockwise. Such non-standard orientations are rarely used in mathematics but are common in 2D computer graphics, which often have the origin in the top left corner and the y-axis down the screen or page.
You can rotate in the opposite direction by applying the transpose of the rotation matrix to the point
Important properties
There are a number of properties which will be useful if remembered, as we develop our physics engine.
unit vector along the x-axis
when multiplied by the rotation matrix returns
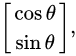
This is the left column of the rotation matrix.
unit vector along the y-axis
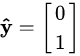
when multiplied by the rotation matrix returns
This is the right column of the rotation matrix.
Direction: Right-handed or Left-handed?
Wiki explains that
The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. −90°). Thus the clockwise rotation matrix is found as (it is simply putting a minus in front of the theta).
The above matrix is actually the transpose of the original matrix.
Application of the Right-handed rule and Left-handed rule
More of a note to myself, as I had to spend a fair bit of time searching the internet to find a concise explanation of what these "handed" systems mean. The only video you need to watch to fully understand this concept is here, which explains (in very concisely) not just one but 3 (!) variations of this method: i) 3 finger method, (ii) curling method, and (iii) palm-pushing method.
With the "3 finger method",
thumb points in direction x,
second fingure points in x,
third finger points in direction z
Hence, if you apply your right-hand to a "maths textbook" cartesian coordinate system, z wil be sticking out of the screen (ie towards you). Most importantly, the Javascript screen coordinate system is left-handed. The z-axis in this case will also be pointing towards you as the y-axis is poitnting downwards.
Phaser 3's various rotation related methods
As you would expect, Phaser 3 provides a lot of methods, specifically to rotate objects by certain angles (ie incrementally by certain angles).
Phaser.Math.Vector2.rotate(delta)
As the name suggests, this method rotates a vector by an angle amount. So for example,
var p = new Phaser.Math.Vector2(5,0)
console.log(p.rotate(Math.PI/4))will return (decimal points abbreviated):
{x: 3.53533, y: 3.53533}Looking at the underlying code, it is doing exactly as described above.
rotate: function (delta)
{
var cos = Math.cos(delta);
var sin = Math.sin(delta);
return this.set(cos * this.x - sin * this.y, sin * this.x + cos * this.y);
}
});Probably because Phaser 3 provides the above method to deal with rotating vectors, it does not seem to provide a generic method for multiplying a vector with a 2x2 matrix (although it does provide a method to apply a 3x3 and 4x4 matrix to a vector).
<static> Phaser.Geom.LineRotate(line, angle)
The documentation says:
Rotate a line around its midpoint by the given angle in radians..
var Rotate = function (line, angle)
{
var x = (line.x1 + line.x2) / 2;
var y = (line.y1 + line.y2) / 2;
return RotateAroundXY(line, x, y, angle);
};The underlying code calculates the mid-ponit of the line then calls another method called RotateAroundXY. As explained earlier, the standard rotation matrix rotates a point around the origin. What the above method is trying to do is rotate the end points of the line around its mid-point, as opposed to the origin. In order to rotate a point around another point that is not the origin, you need to first "translate" the point (to be rotated), apply the rotation matrix, then translate it back by the same amount - which is what RotateAroundXY does.
<static> Phaser.Geom.LineRotateAoundXY(line, x, y, angle)
var RotateAroundXY = function (line, x, y, angle)
{
var c = Math.cos(angle);
var s = Math.sin(angle);
var tx = line.x1 - x;
var ty = line.y1 - y;
line.x1 = tx * c - ty * s + x;
line.y1 = tx * s + ty * c + y;
tx = line.x2 - x;
ty = line.y2 - y;
line.x2 = tx * c - ty * s + x;
line.y2 = tx * s + ty * c + y;
return line;
};Play around with rotating Phaser Geom Line
Comments