Understanding 2D Physics Engines with Phaser 3, Part 17.1: Collision Response with Rotation

Capsule to Capsule Collision response with Rotation

Having dealt with the concepts of center of mass and mass moment of inertia, we finally turn to the subject of collision response with rotation. For our first attempt we will experiment with a pair of capsules.

The basic necessary steps to implement collision response with rotation are:

1. to detect the collision, identify the depth of penetration, the collision normal and the contact point

2. separate the objects by changing their positions by the depth of penetration along the collision normal

3. apply impulse to the objects to change their velocities

The entirely new elements are: (i) identifying the contact point, and (ii) calculating the impulse that affects the angular velocity. Both of these elements are quite challenging.

Collision detection

In prior posts, I covered two different ways of detecting collisions between capsules.

1. Looking for the closest points on the pair of capsules (i.e., if the distance between the closest points is less than 0, then the capsules are intersecting),

2. Separating axis theorem

As we have seen, we can obtain the collision normal with either of the methods.

Getting the contact point however, is a bit tricky. Contact point generation is a big topic in itself but for the purposes of this post - the main purpose of which is to code collision response with rotation - we will adopt the first collision detection method since it is easy to customise it to get contact point information.

Getting the contact points

As mentioned above, the first of the collision detection methods involves finding the "closest" distance between the capsules. This was done by looking for the shortest distance between the 4 "circle centers" against the "spine" of the other capsule.

The collision detection implementation left you with not only the distance but the pair of points that made up the nearest distance. Specifically, the pair of points are the relevant end cap center and the nearest point on the "spine" of the other capsule. The vector between the points is the collision normal.

But where is the contact point? This is a bit confusing because in the real world, rigid bodies do not intersect but in the world of computer simulations, they do - like in the above diagram. One easy way to eliminate this confusion is simply to separate the bodies by moving them apart so that the contact point is clear, like below.

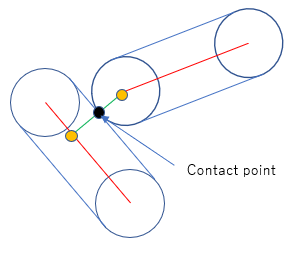
Or you can "estimate" the contact point based on some logic. We could extrapolate along the collision normal from the center or nearest point on the spine by relevant end cap radius to get a contact point. If we do this for each of the bodies, we can get a contact point "estimate" for each, like below. If the depth of penetration is small these contact points would be very close.

I have refactored the code a little bit since we last dealt with this, but the algorithm remains the same.

The main intersection code is below:

class Intersects {
  
  static  CapsuleToCapsule(capsuleA, capsuleB, manifold) {
   
    let {distance: distance, points: PT} = Distance.BetweenCapsules(capsuleA, capsuleB);
    if (distance <= (capsuleA.radius+capsuleB.radius)) {     
      manifold.depth = (capsuleA.radius+capsuleB.radius) - distance;
      manifold.normal = new Phaser.Math.Vector2(PT[0].x-PT[1].x, PT[0].y-PT[1].y).normalize();
      manifold.points[0] = PT[0].add(manifold.normal.clone().scale(capsuleA.radius));
      manifold.points[1] = PT[1].subtract(manifold.normal.clone().scale(capsuleB.radius));
      return true;
    }
    else
    {
      return null      
    }
  }
}

The key piece of code that deals with finding the "nearest points" between two capsules is below.

// finds the closest distance between a pair of capsules
// returns the actual distance and the array of the end points of the separation
// points[0] = nearest point on capsuleA and  points[1] = nearest point on capsule B
class Distance {

  static BetweenCapsules(capsuleA, capsuleB) {
  
    let checkPair;
    checkPair = Segment.getNearestPoint(capsuleA.getPointA(), capsuleB);
    let shortestDist = checkPair.dist;
    let closestPoints = [capsuleA.getPointA(), checkPair.point];
    checkPair = Segment.getNearestPoint(capsuleA.getPointB(), capsuleB);
    if (checkPair.dist<shortestDist) {
      shortestDist = checkPair.dist;
      closestPoints = [capsuleA.getPointB(), checkPair.point];
    }
    checkPair = Segment.getNearestPoint(capsuleB.getPointA(), capsuleA);
    if (checkPair.dist<shortestDist) {
      shortestDist = checkPair.dist;
      closestPoints = [checkPair.point, capsuleB.getPointA()]
    }
    checkPair = Segment.getNearestPoint(capsuleB.getPointB(), capsuleA);
    if (checkPair.dist<shortestDist) {
      shortestDist = checkPair.dist;
      closestPoints = [checkPair.point, capsuleB.getPointB()]
    }
    
    return {distance: shortestDist, points: closestPoints}
  
  }
  
}

Main Game Loop

The main loop remains the same as before. We loop through pairs of bodies, finding pairs that are intersecting.

for (let i = 0; i < this.bodies.length; i++) {
      const body1 = this.bodies[i]
      for (let j = i + 1; j < this.bodies.length; j++) {
        const body2 = this.bodies[j]
        let manifold = new Manifold(body1, body2);
        if (Intersects.CapsuleToCapsule(body1, body2, manifold)) { 
          body1.isColliding = true;
          body2.isColliding = true;
          ContactSolver.Separate(body1, body2, manifold);
          this.responseCaps2Caps2(body1, body2, manifold);
        }
      }  

For pairs that are intersecting, we first separate the bodies so that they are just touching, by calling the following code.

class ContactSolver {
  
  static Separate(capsuleA, capsuleB, manifold) {
    
    let sepFactor = manifold.depth / (capsuleA.inv_m + capsuleB.inv_m);
    capsuleA.translate(manifold.normal.clone().scale(capsuleA.inv_m*sepFactor));
    capsuleB.translate(manifold.normal.clone().negate().scale(capsuleB.inverse_mass*sepFactor));
    
  }
  
}

Then comes the next challenge. Calculating the impulse to effect the collision response. That will be covered in the next post.