Rotation in a plane
So far we have dealt with circles and axis-aligned boxes. Collision detection, resolution and response becomes considerably more complex as soon as rotation is introduced. In this post I review the key background concepts necessary to implement simulation of moving bodies with rotation around the screen.
Rotation Motion
Consider the following circle rotating about its centre, in the anti-clockwise direction (it is assumed that we are working in the "normal" cartesian coordinate system, i.e. the "right-handed" coordinates).
In talking about the rotational equivalent of the various basic equations, it is useful to summarise the typical notation used in rotational dynamics.
Linear | Angular | |
Displacement | x | θ |
Velocity | v | ω |
Acceleration | a | α |
Mass | m | Ι |
Force | F = ma | τ = Ια |
Angular Velocity
Change in angular displacement per unit time is called angular velocity. The symbol for angular velocity is ω and the units are typically rad per second.
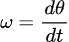
Angular speed is the magnitude of angular velocity. In 2D, ω is a scalar.
Linear Velocity of a specific point of a rotating body (with no translational motion)
We also have the concept of velocity at a particular point of a rotating body. Referring to the above diagram again, you can intuitively understand that point p1 is moving "upwards". How is this calculated?
By definition, the relation between angular displacement (θ) and linear displacement (= along the circumference by point p) denoted by s is:
Plugging in the above into the definition of linear velocity gives us the following relationship.
You can see from the above relationship that even if θ is constant, v will differ based on r. If you refer to points p1 and p2 on the diagram above, this should intuitively make sense - p1 which is further away from the centre you would expect to be moving faster than p2, which is close to the centre.
To date, we have referred casually to a single value for velocity - we were in fact referring to the velocity of the body at its centre of mass. If the body is not rotating, the velocity at any point on the body would be the same. However, if it is rotating, the speed at a particular point would be different from the speed at another point.
When dealing with rotating objects it is important therefore to be aware of what velocity we are dealing with. Practically speaking we need to know the distance from the centre of mass, which is typically denoted by r. r is a vector from the center of mass (COM) to a particular point on an object. r can be thought of as referring to a "radius" from COM to a point. Every single unique point on an object will require a different r.
'Direction' of angular velocity
In the case of the diagram above, if dθ is positive, i.e. angular displacement is anti-clockwise, ω is positive.
Imagine that we are working the real world of 3D, and you are looking at the "disc" from "above. The disc would be rotating counterclockwise. However, now image looking at the disc from "below" - the disc is now spinning clockwise!
If working in 3D it is critical to be precise about the "direction" of rotation, and sometimes it is helpful even when working exclusively working in 2D, to define the rotation in terms of vectors that represent the "axis of rotation".
Referring to the "3D" diagram above, would be defined as a vector in the positive upward z-direction with magnitude of ω. The direction would be determined by the right-hand rule (stick your thumb in the direction of the axis of rotation and "curl" your fingers - the curled fingers point in the direction of rotation).
The equation given above for the linear velocity now becomes a cross product between ω and r. It is important to be consistent about the direction of r - I have defined r as being a vector that points away from the origin to the point.
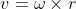
Vector cross product version
In 2D ω is most certainly only expressed as a scalar. So how do we end up with a velocity with direction? We can start by expressing both ω and r as a 3D vectors:
ω: zeros for the x and y components, and z=ω. Now we have two vectors.
r: z-component set to zero
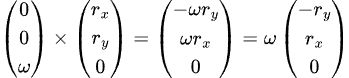
This is the basis for the following "hack" used to return the velocity vector facing the correct direction, as per Chris Hecker:
where the subscript upside down T is the perpendicular operator (not to be confused with the superscript T which represents transpose of matrix!), that turns r and rotates it counterclockwise by 90 degrees (in a right-handed coordinate system).
Cross product matrix version
In some tutorials, the above formula is expressed in terms of cross product matrix as follows:
where Rs is referring to the anti-symmetric matrix of r.
Linear Velocity of a specific point of a rotating body with translational motion
As stated above, the velocity of a particular point of a body depends on the radius from the centre of mass. What of bodies that are simultaneously rotating and translating at the same time? As explained by Chris Hecker in his article here, we can rely on the Chasles' Theorem to break up the motion into linear and angular components and come up with the following equation which gives the linear velocity of a point of a body that is rotating and translating at the same time.
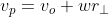
Useful References
https://en.wikipedia.org/wiki/Rotation_around_a_fixed_axis