The Cross Product
Some mathematicians will tell you that the vector cross product does not exist in 2D. If you search for a wiki page on cross product, there is a page for cross product of vectors in 3D space, but nothing specifically about 2D.
However, if you start looking at tutorials of 2D physics engines, you will see references to cross products, particularly as you get into moving rotating shapes around the screen.
In fact, there is even a cross product method provided by Phaser 3 for its Vector2 class.
cross: function (src)
{
return this.x * src.y - this.y * src.x;
},Of course, there is a cross product method for Phaser's Vector3 class.
cross: function (v)
{
var ax = this.x;
var ay = this.y;
var az = this.z;
var bx = v.x;
var by = v.y;
var bz = v.z;
this.x = ay * bz - az * by;
this.y = az * bx - ax * bz;
this.z = ax * by - ay * bx;
return this;
},The immediate thing you will notice is that Phaser's vector2 cross product method returns a scalar, whereas the vector3 cross product returns a 3D vector.
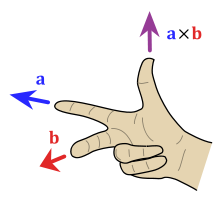
Geometric understanding
In trying to understand what a cross product means in 2D, it is useful to understand the geometric understanding of vector cross product in 3D.
The following is reproduced from WIki.
The cross product a × b is defined as a vector c that is perpendicular (orthogonal) to both a and b, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span.
The cross product is defined by the formula
The 3D cross product will be perpendicular to the plane.
Going back to the puzzle of cross product in 2D...
The Phaser's vector2 cross product is reproduced below (I've written 2d vectors as column matrices):
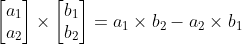
and similarly, Phaser's vector3 cross product can be expressed as below..
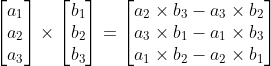
Magnitude of 3D Vector Cross
When you look at the output vector from the 3D cross product with the scalar output from the 2D cross product, you will see that the 2D cross product output is the same as the z-value of the 3D cross vector. In effect, 2D vector cross product is the same as extending the 2D vectors into 2D by assuming z-values as zero, ie:
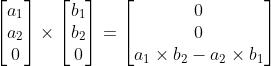
Since x and y values are always zero, you could say that 2D vector cross is the magnitude of the vector output (which is pointing along the z-axis) of the two vectors in the x-y plane.
Cross Product 2D = determinant of 2x2 matrix
Sometimes the cross product of two products in the x-y plane is expressed as the determinant of the 2x2 matrix built from the two vectors
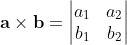
Perpendicular Dot Product
And some express the 2D vector cross as the perpendicular dot product, meaning:
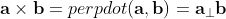
where the perpendicular of a is given by simply swapping the x and y elements and negating one of the elements.
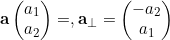
This last expression may be the most intuitively easy to understand expression of them all.
This will make much more sense when we come to dealing with angular velocities, and in particular calculating the linear velocity of a point of a rotating shape.
2D vector cross that return 2D vector
You will also come across physics 2D engine tutorials with code that involves cross product between a scalar and a vector that returns a 2D vector, implemented as:
Vector2D CrossProduct(s, v)
{
return new Vector2D(-s * v.y, s * v.x);
}
or
Vector2D CrossProduct(s, v)
{
return new Vector2D(s * v.y, -s * v.x);
}This is simply rotating the vector by 90 degrees, then scaling it by the scaler.
Useful cross product properties / identifies
Cross product with itself is the zero vector
From definition, cross product of two parallel vectors (co-linear) is zero as sine of 180 or 0 degrees is zero.
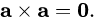
Anticommutative
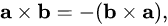
Distributive over addition
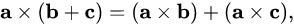
Triple product expansion
Scalar triple product
The scalar triple product of three vectors is defined as
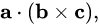
with the following property:
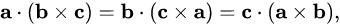
Vector triple product
The vector triple product is the cross product of a vector with the result of another cross product, and is related to the dot product by the following formula
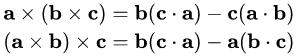
You will find that this is useful in understanding why there are slightly different looking expressions of effective mass that appears in the calculation of collision response.
Cross Product Matrix
Finally, I will introduce the concept of cross product matrix (in 3D), as this term will sometimes make an appearance in physics engine tutorials.
(From wiki here)
The vector cross product also can be expressed as the product of a skew-symmetric matrix and a vector:
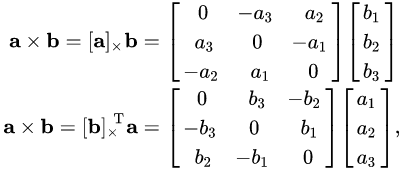
We can force a 2D vector into the above as follows:
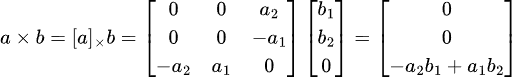
Which, as you would expect returns a vector perpendicular to the plane that would be formed by the 2D vectors a and b, with the magnitude consistent with the 2D cross product formula given above.
Comments