
Before continuing our challenge to derive the mmoi for other shapes, I will introduce two important theorems that will help us as we deal with more complicated shapes.
Perpendicular Axis Theorem
The moment of inertia of a plane area about an axis normal to the plane is equal to the sum of the moment of inertia about any two mutually perpendicular axes lying in the plane and passing through the given axis.
That means the moment of inertia Iz = Ix + Iy.
Parallel Axis Theoerm
The moment of inertia of an area with respect to any given axis is equal to the moment of inertia with respect to the centroidal axis plus the product of the area and the square of the distance between the two axes.

MMOI of Rectangular Lamina
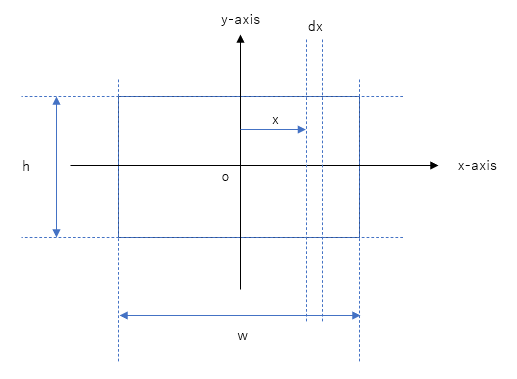
We are going to derive the mmoi of a rectangular lamina rotating around the z-axis through the centre of mass as shown below.

We will drive the mmoi in two different ways:
calculating the mmoi around the x-axis and mmoi around the y-axis, then using the perpendicular axis theorem, and
directly deriving the mmoi around the z-axis.
First, we will calculate the mmoi around the y-axis. To do so, we assume a rectangular strip of width dx for the "element", as shown in the diagram below.
Using the perpendicular axis theorem
The density of the lamina is the total mass divided by the area.

The area of the elemental strip is the product of the height and the width.

From the above, it follows that:

Plug the above into the mmoi equation

Similarly, mmoi around the x-axis would be:

It follows from the perpendicular axis theorem that:

Sometimes you would find the moment of inertia around the axis perpendicular to the plane through the centre of mass expressed as J, although in our 2D physics engine, our bodies would only rotate around the z-axis, there is no need to be this prescriptive.

Direct calculation of mmoi around z-axis
We assume that the "element" is a "point" of density ρ. The perpendicular distance of this element from the z-axis is given by the square root of (x^2+y^2).
Hence the mmoi can be calculated as a double integral as follows.

We can perform the integral one by one. Taking the inner one first:

Then we can perform the outer integral, to eventually get the same result:

コメント