Understanding 2D Physics Engines with Phaser 3, Part 4: Circle Collision Response with Mass
- cedarcantab
- Feb 22, 2022
- 5 min read
Collision Response in Circle2Circle with mass
In the previous post I developed the crudest form of collision response; that of two circles of equal mass bouncing off each other in a perfectly elastic manner.
In this post, I take it a bit further by developing the concept of impulse and introducing coefficient of elasticity (restitution).
For the actual coding of collision response, I relied pretty much entirely on this paper by Chris Hecker here which I wish I had come across earlier as it would have let me avoid a lot of heartache.

Reminder about Impulse
We covered the concept of impulse in the very early posts of this series (here).
The most important points to remember are:
momentum is the product of a body's mass and velocity
impulse is the change in momentum.
Since mass remains constant, and we know the velocities of the bodies before the collision, if we can calculate the impulse, we can calculate the velocities of the bodies after the collision.
Quick review of Coefficient of Restitution (COR)
Another concept that we will introduce in this version of collision resolution is coefficient of restitution. Put simply, it is the bounciness of the objects.
Put in more difficult terms, restitution describes how much energy is left after each collision. The ratio between the starting and ending velocity after a bounce is called coefficient of restitution, or COR.
Objects with a COR of 0 would absorb all energy on impact, like a bag of sand hitting the floor.
Objects with a COR of 1 would have perfect elasticity, like a super bouncy bouncing ball.
Objects with a COR > 1 are completely fictional and would add extra energy after each collision.
This may be expressed mathematically by the following equation.
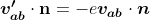
What if two objects with different COR collide? In such a case, the lowest restitution will count. This intuitively makes sense if you image a bouncy ball hitting a bag of sand. In this case, neither the bouncing ball or the bag of sand will bounce, they both inherit the restitution of the bag (zero).
Coding the Collision Response
There are lots of different ways of coding the collision response. I will adopt the impulse method since it's backed up by physics laws.
In terms of how to code it, I have found the explanation in this paper by Chris Hecker here really concise and easy to understand. I very much encourage you to read the paper, but I have jotted down the important bits to make it easier to understand how I have coded it.
Notation
First of all, as indicated in the above diagram taken from Chris Hecker's paper, the collision normal is pointing towards object a - this is the opposite of the convention I used in the previous post.
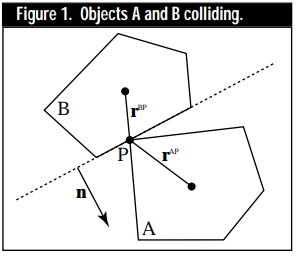
I have amended my collision detection routine to be consistent with this, so that I can use the formulae from the paper as they are described, without changing any of the signs.
intersectCircleToCircle(circleA, circleB, manifold) {
const distance = Phaser.Math.Distance.BetweenPoints(circleA, circleB);
manifold.depth = (circleA.radius + circleB.radius) - distance;
manifold.normal.set(circleA.x - circleB.x, circleA.y - circleB.y).normalize();
return (manifold.depth >= 0)
}
Relative Velocity
As explained in this site here, if you have objects a and b moving with velocities Va and Vb, the velocity of object a relative to the object b is expressed as below (we worked through this in the previous post, but I mention it here again since typically relative vector ab would refer to a vector pointing from a to b), but where we are referring to relative velocity of body a and body b, we must make sure to get the "direction" correct.
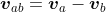
Change in Velocity is Impulse
We are trying to find the velocity of the objects after the collision. The difference between the post-collision velocity and the pre-collision velocity, is, by definition, impulse / mass.
If we start by expressing impulse with a scalar j times the normal vector, then by definition, the following will be true (this is just writing out the definition of impulse)
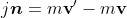
If we jumble it up and little bit then we can write the following for the two colliding objects
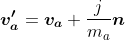
(Post collision velocity of object a)

(Post collision velocity of object b)
Note how you are adding the impulse (divided by mass) to the velocity a, whereas you are subtracting the same impulse (divided by mass) to velocity b. In order for this to work, you need to have the collision and the relative velocity (which is used to calculate j) "pointing" in consistent direction per Chris Hecker's paper.
Subtracting the lower equation from the upper equation gives:
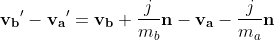
Combing the above with the equation of the coefficient of restitution gives:
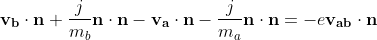
If you work through this, you end up with:
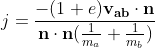
Taking a look at the above equation, you will note that the numerator (-(1+e)Vab.n) is the relative velocity along the collision normal, taking into account the coefficient of restitution, or sometimes referred to as the total velocity of the collision.
How do we calculate the post collision velocity??
So how do we calculate the post collision velocity of a and b? Refer back to the equations defining the impulse in the middle of the derivation above, reproduced below;
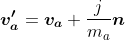
(Post collision velocity of object a)

(Post collision velocity of object b)
We have the equation to arrive at the scalar of the impulse j which we can put into the post collision velocity equations above to get what we want!
In calculating j, there is a dot product of the normal vector with itself in the denominator. In my code, the collision normal vector is normalised when calculated. A unit vector dotted by itself is 1 so we can ignore it.
Putting the above equations into words, each body is being applied an impulse along the collision normal and each body will end up gaining some velocity along the collision normal proportionally to their inverse mass, thereby moving the bodies apart at different velocities. Another important point to note is that the impulses are scaled by inverse masses so that the momentum of the system is conserved.
We can implement the above very easily, given that we have the normal vector and the pre-collision velocities of the two circles.
responseCircleToCircle(circleA, circleB, manifold) {
let relativeVelocity = new Phaser.Math.Vector2(circleA.velocity.x - circleB.velocity.x, circleA.velocity.y - circleB.velocity.y);
//separation speed - relative velocity vector projected onto the collision normal vector
let separatingSpeed = relativeVelocity.dot(manifold.normal);
if (separatingSpeed > 0) return; // if already moving apart no need to do collision response
let e = Math.min(circleA.restitution, circleB.restitution);
let j = -(1 + e) * separatingSpeed / (circleA.inverse_mass + circleB.inverse_mass );
let impulse = manifold.normal.clone().scale(j);
circleA.velocity.add(impulse.clone().scale(circleA.inverse_mass));
circleB.velocity.subtract(impulse.clone().scale(circleB.inverse_mass));
}Example Code
Useful Reference
http://www.chrishecker.com/images/e/e7/Gdmphys3.pdf (this has all the information you need for coding basic collision response)
https://research.ncl.ac.uk/game/mastersdegree/gametechnologies/physicstutorials/5collisionresponse/Physics%20-%20Collision%20Response.pdf (this is another great article which gives a more "intuitive" explanation of the impulse method)
https://www.youtube.com/watch?v=1L2g4ZqmFLQ (content if same as paper above but in video)
https://www.youtube.com/results?search_query=science+abc+bouncy (very good video on coefficient of restitution)


Comments