Understanding 2D Physics Engines with Phaser 3, Part 5: Circle vs Line Collisions
- cedarcantab
- Feb 28, 2022
- 6 min read
Updated: May 7, 2023
Handling collisions between Circle and Line
We covered the topic of colliding circles against axis aligned lines. In this post we cover the very much more complex topic of colliding circles against non-axis aligned lines.
Just as in the case of circle to circle collision handling, we can break the problem down into the following 3 basic steps.
collision detection: assess if circle has intersected against the line segment, find the normal collision vector and the depth of the collision
collision resolution: separate the objects apart along the collision normal by the depth of penetration = collision resolution, and
collision response: change the velocity of the objects by reference to the relative velocity of the 2 bodies along the collision normal.
The step that is most different from the circle to circle situation is step 1. Once we figure out the collision normal and the depth of penetration (i.e. detect the collision and get the collision manifold data), then steps 2 and 3 are relatively straightforward.
Detecting collision between Circle and Line
The key step in detecting collision between a circle and a line is finding the nearest point on the line from the centre of the circle. If the distance between the centre of the circle and this "nearest point" is less than the radius of the circle, it means that the circle is colliding with the line.
But how do we find this nearest point? It is relatively easy to figure this out if we draw what is intuitively an obvious relationship between the point and the line.
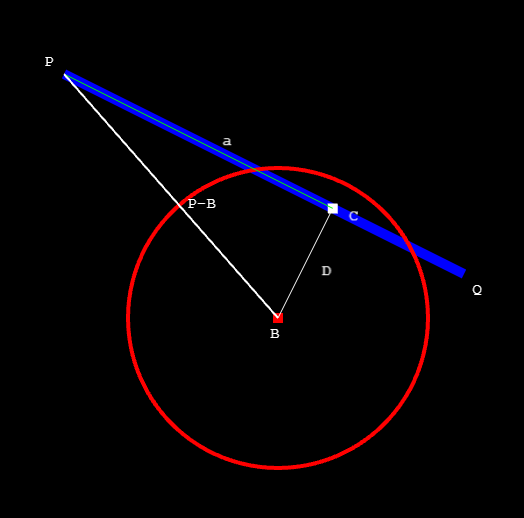
The thick blue line represents the line, and the red square is the center of the circle, labelled B. We want to find the point on the blue line PQ that is nearest to B - in the above diagram it is labelled C.
You can see that C is P + the projection of (P-B) onto (P-Q). And we know how to do projections - we can use the dot product.
More specifically, the dot product gives the scalar projection of a vector along another vector, in the direction of the given vector. So (P-B) dotted against (Q-P) would give the scalar projection PC (call it a). Just be careful about the direction of the vectors and the sign of the scalar projection - in this particular case it would be a negative number since the vectors are pointing in opposite directions.
For ease of reference against Phaser 3 methods, let us define the various points as follows:
P = (x1, y1)
Q = (x2, y2)
B = (point.x, point.y)
Then C can be calculated as follows.
C = P + [(P-B)dot(P-Q)](normalized(P-Q)/||P-Q||
= P + [(P-B)dot(P-Q)](P-Q)/||P-Q||^2
= (x1, y1) + (point.x-x1, point.y-y1)dot(x2-x1, y2-y1)/||(x2-x1, y2-y1)dot(x2-x1, y2-y1)
= (x1, y1) + [(point.x-x1)*(x2-x1)+(point.y-y1)*(y2-y1)]/[(x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)]
Apart from the sign of scalar projections, another thing you need to be careful about is the case where B is "outside" the line segment, then the "projected" intersection point will fall outside the line segment if you follow the above process. In this situation, you need the "end point" of the line segment closest to the ball.
The code to generate the graphical explanations above are accessible in Codepen below.
Relevant Phaser 3 methods
If you look through the methods relating to Geom Line object, Geom Circle object and Geom.Intersect class, you will come across a number of methods that are named as if they will do what we want, including the following.
Phaser.Geom. Line.GetNearestPoint(line, point [, out])
Phaser.Geom.Intersects.GetLineToCircle(line, circle [, out])
Phaser.Geom.Intersects. LineToCircle(line, circle [, nearest])
Let's look at the 1st and 3rd methods in detail.
Phaser.Geom. Line.GetNearestPoint(line, point [, out])
Documentation states that this method "Get the nearest point on a line perpendicular to the given point."
var GetNearestPoint = function (line, point, out) {
if (out === undefined) { out = new Point(); }
var x1 = line.x1;
var y1 = line.y1;
var x2 = line.x2;
var y2 = line.y2;
var L2 = (((x2 - x1) * (x2 - x1)) + ((y2 - y1) * (y2 - y1)));
if (L2 === 0) {
return out;
}
var r = (((point.x - x1) * (x2 - x1)) + ((point.y - y1) * (y2 - y1))) / L2;
out.x = x1 + (r * (x2 - x1));
out.y = y1 + (r * (y2 - y1));
return out;
};The red line is calculating the squared of the length of the line segment, storing it in variable L2 (there is a useful check to make sure this is not zero - ie the line is not a line, but a point - in which case, a (0,0) is returned).
The blue line is the dot product between the "point to the start of the line segment" vector against the line segment, divided by L2 => hence this gives the scalar projection of the point onto the line.
The black bold lines is adding the line segment vector * scalar projection calculated, to the start of the line to get the "nearest point".
The last two lines of code (reproduced below) is in fact, the line passing through points A=(x1, y1) and B=(x2, y2) expressed in the explicit form of a line.
out.x = x1 + (r * (x2 - x1));
out.y = y1 + (r * (y2 - y1));
which is
L(r) = A + r(B-A)
Very simple.
Unfortunately, we cannot use this method as is, since, as the name suggests, this gets the nearest point on the line (which extends indefinitely in both direction), whereas we want the "nearest point" to be within the two ends of the segment.
In order to make sure that the nearest point actually fall on the line segment, the variable r needs to be clamped between 0 and 1.
Phaser.Geom.Intersects.LineToCircle(line, circle [, nearest])
The documentation states that this method "Checks for intersection between the line segment and circle." Exactly what we want.
If you look at the underlying code, you will find that it is basically following the logic described above. Essentially, lc is the vector which joins the center of the circle to the beginning of the line segment, d is the line segment, and the dot project of lc and d is p. The Phaser code uses another method called Contains to check whether the point is within the circle, but the logic is the same.
var LineToCircle = function (line, circle, nearest)
....
var dx = line.x2 - line.x1;
var dy = line.y2 - line.y1;
var lcx = circle.x - line.x1;
var lcy = circle.y - line.y1;
// project lc onto d, resulting in vector p
var dLen2 = (dx * dx) + (dy * dy);
var px = dx;
var py = dy;
if (dLen2 > 0) {
var dp = ((lcx * dx) + (lcy * dy)) / dLen2;
px *= dp;
py *= dp;
}
nearest.x = line.x1 + px;
nearest.y = line.y1 + py;
// len2 of p
var pLen2 = (px * px) + (py * py);
return(pLen2<=dLen2&&((px*dx)+
(py*dy))>=0&&Contains(circle,nearest.x,nearest.y));In working through the logic above as well as the Phaser 3 methods, you will note that at some point during the code, all the information necessary for collision resolution is obtained:
the collision point (the nearest point),
depth of penetration (distance of D - radius of the circle) and
the collision normal.
Having said that, the Phaser provided methods do not actually return us with all the information we require (although they are all calculated along the way), so I have created the following method to detect collision and return the information in a "collision manifold" object.
Collision manifold
Declare a variable to hold the collision manifold, like so.
let manifold = {normal: new Phaser.Math.Vector2(0), depth: Number.MAX_VALUE, cp: new Phaser.Math.Vector2(0) }; Method to detect collision
The above, together with the circle and the line is passed to the following method.
intersectCircleToLine(circle, line, manifold) {
manifold.cp = this.nearestPointOnLine(line, circle);
manifold.normal = new Phaser.Math.Vector2(circle.x - manifold.cp.x, circle.y - manifold.cp.y);
let distance = manifold.normal.length()
manifold.depth = circle.radius - distance;
manifold.normal.normalize();
return (manifold.depth > 0)
}
nearestPointOnLine(line, circle) {
//returns with the closest point on a line segment to the centre of circle
let out = new Phaser.Geom.Point();
let x1 = line.x1;
let y1 = line.y1;
let x2 = line.x2;
let y2 = line.y2;
let L2 = (((x2 - x1) * (x2 - x1)) + ((y2 - y1) * (y2 - y1)));
let r = (((circle.position.x - x1) * (x2 - x1)) + ((circle.position.y - y1) * (y2 - y1))) / L2;
r = Phaser.Math.Clamp(r, 0, 1);
out.x = x1 + (r * (x2 - x1));
out.y = y1 + (r * (y2 - y1));
return out;
};And with the pieces of information returned in the collision manifold, the the logic for the collision resolution and response are quite similar to what we have done with circle to circle collision. In the example code I created, the line does not move so the resolution and response is all done by the circle.
Collision Resolution
In the example I created, I have assumed that the line is a "wall" and is immobile, hence the resolution is achieved by moving the circle in the direction of the collision normal by the depth of penetration.


Comments