Center of Mass of Lamina: Isosceles triangle

We will put the learnings of the previous post into practice by applying the principles to a triangle.

Center of Mass of a Triangle

We will consider an isosceles triangle, with its base aligned with the x-axis and symmetrical around the y-axis as below, and determine the centroid (x,y), with a base of b and height of h.

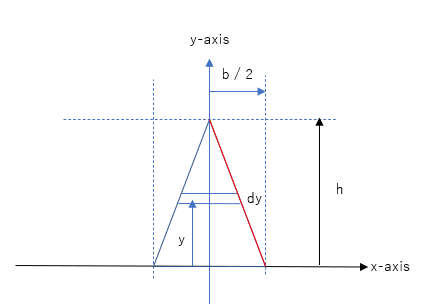
Since it is intuitively obvious that the x coordinate of the centroid is 0, we will focus our efforts on calculating the y-coordinate of the centroid.

Consider the right half of the triangle

In order to make the calculation a little easier, we will also only consider the right half of the triangle - hopefully it is clear that the y-coordinate of the centroid for half of the triangle is the same as that of the whole.

Before we get integrating..

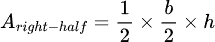
(Everything from here onwards will be with respect to the right half of the triangle, unless otherwise specified).

the equation for the "edge" highlighted in red is:

which means that:

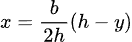
The y-coordinate of the centroid is:

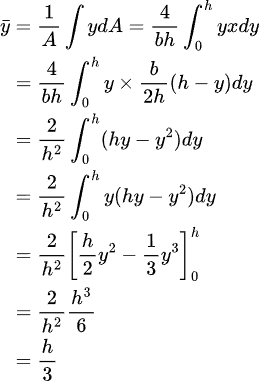
In other words, the y-coordinate of the centroid of a isosceles triangle is a third way up from its base.