Understanding 2D Physics Engines with Phaser 3, Part 11.2: SAT - Minimum Translation Vector

Minimum Translation Vector

In the previous post we look at how to implement a basic separating axis theorem to detect intersection between two polygons.

With a bit of additional code, this algorithm can give you what is referred to as the minimum translation vector, or MTV. This is basically a vector,

1. whose length is the depth of penetration, and

2. direction is the collision normal.

With such a vector, by moving the polygons away from each other by the depth of penetration in the direction of the mtv, you can make them just separate.

So how do we the MTV?

Depth of penetration

The depth of penetration is actually the overlap of the intervals. We have explored in some depth how to determine the depth of overlap, in the post on AABB collision detection. However we will do a quick recap.

Consider the following situation.

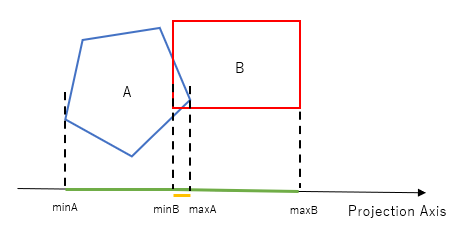
The depth of overlap is maxA - minB.

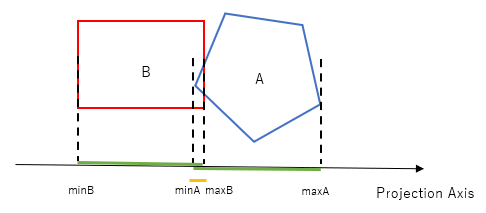
However, consider the following situation. The formula above clearly does not give you the overlap. The formula for the overlap is maxB - minA.

In otherwords:

1. If polygon B is to the right of polygon A, depth of penetration = maxA - minB

2. If polygon A is to the right of polygon B, depth of penetration = maxB - minA

In the post on AABB collision detection we saw that the overlap can be obtained by:

Math.min(maxA.x, maxB.x) - Math.max(minA.x, minB.x)

which can be implemented as follows.

class Interval {
  constructor(min = Number.MAX_SAFE_INTEGER, max = Number.MIN_SAFE_INTEGER, vertex = new Phaser.Math.Vector2()) {
    this.min = min;
    this.max = max;
    this.vertex = vertex;
  }
 
  getOverlap(interval) {
    return Math.min(this.max, interval.max) - Math.max(this.min, interval.min);
	}

There are other ways to identify the overlap. For example, if you know that the polygons are overlapping, we can use a simpler formula below to get the overlap. It should be understood that this will not give the right result if the polygons are separated.

 Math.min(maxB - minA, maxA - minB)

You want the minimum overlap

and as the name suggests, we want the minimum overlap. So in SAT code that loops through the projection axes, you want to keep looking for the shortest overlap.

 sat(polygonA, polygonB, manifold) {  
   
    var n = null;
    var overlap = Number.MAX_SAFE_INTEGER

    let axes1 = polygonA.getAxes();    
    for (let i = 0; i < axes1.length; i++) {     
      const axis = axes1[i];
      const intervalA = polygonA.projectVertices(axis);
      const intervalB = polygonB.projectVertices(axis);
      var o = intervalA.getOverlap(intervalB);
      if (o < 0) {
        return false;
      } 
      
      if (o < overlap) {
        overlap = o;
        n = axis;
      }
    }

Note in the above code that when a "shorter" overlap is found, we store not only the overlap, but also the projection axis. This information is needed to get to the MTV.

The same process needs to be performed for projection axes from Polygon B.

Direction of the minimum translation vector

Once the above loops have been executed (and the polygons are indeed intersecting), we would have:

1. the projection axis (vector2) associated with the smallest interval overlap

2. the actual value of the overlap

Intuitively one can guess that the minimum translation vector would be along the projection axis - that is why we store the projection axis associated with the minimum interval overlap - in the below situation, the yellow bar would represent the MTV.

Direction of the MTV

In the above situation, the MTV would be the projection axes from polygon B. The projection axes are the outward facing normal of each edge. In the above scenario, the projection axis could have been the collision normal of either of the vertical edges. In otherwords, it could be facing left or right.

However, in order for the MTV is to be useful, we want the direction of the MTV to be consistent, ie we want to know in advance that the MTV would pointing from polygon A away from polygon A (or from polygon A towards polygon B - doesn't matter which, so long the resulting MTV follows a consistent rule).

How do you make sure consistency in direction?

The easiest way to simply take the vector from the center of the two polygons and point the MTV in the same direction.

In the following implementation,

1. we calculate a vector pointing from polygon A to polygon B.

2. if n (the projection axis) is pointing in the opposite direction, negate it

    // make sure the vector is pointing from polygonA to polygonB
    var cA = polygonA.position.clone();
    var cB = polygonB.position.clone();
    var cToc = cB.subtract(cA);
    if (cToc.dot(n) < 0) {
      n.negate();
    }
  

Finally we store the MTV data in the collision manifold object, and return true to indicate that there is intersection.

// fill the penetration object
manifold.normal = n.clone();		
manifold.depth = overlap;
return true

Collision Separation

Having obtained the MTV, we can separate the polygons. Since the MTV is pointing from Polygon A towards polygon B, we want to move polygon A in the opposite direction to the MTV, and polygon B in the same direction by the MTV. The amount to separate to two polygons is the depth of penetration. In terms of how you allocate the depth of penetration displacement to the two polygons, I have apportioned them according to their inverse masses in the below implementation. However you could simply halve the total and move the polygons by equal amounts.

  resolveCollision(polygonA, polygonB, manifold) {
  
    let sepFactor = manifold.depth / (polygonA.inverse_mass + polygonB.inverse_mass);

    let dA = manifold.normal.clone().scale(-polygonA.inverse_mass*sepFactor);
    let dB = manifold.normal.clone().scale(polygonB.inverse_mass*sepFactor)
  
    polygonA.translate(dA.x, dA.y);
    polygonB.translate(dB.x, dB.y);
 
  }

Lots of different ways to implement

As described above, SAT works through all the edges for both the polygons, but exits the test if a separating axis is found (i.e. the polygons are not intersecting). Put another way, if no separating axis is found (i.e. there is intersection) the method ends up working through ALL the vertices, edges, and both polygons. It means that the more intersecting polygons, the worse the performance.

There are lots of ways of making the code more efficient.

One way of potentially reducing the checking is to calculate a "circle" that bounds the respective polygons and carry out circle to circle collision check before getting into SAT.

If for example you restricted the polygon to rectangles, you would not need to test all the edges, since the parallel edges would yield the same result.