In the prior post started our exploration into the world of constraint solvers by looking at constraint functions.
In this post we will work through this with an example, the contact constraint or the non-penetration constraint.
Non-Penetration Constraint
Imagine two bodies, body 1 and body 2, moving with linear velocities v1/v2, and angular velocities ω1/ω2, that have collided (penetrated) at contact point p as follows.
Position Constraint Function
We can express the contact point for body 1 and body 2 as follows:
In the real world, there would be no "overlap" between two rigid bodies, hence there would be no separate p1 and p2. However, in physics simulations, bodies do overlap (penetrate each other) so that there is a "gap" between p1 and p2. This "gap" must be reduced to zero so that the bodies are not overlapping - this is resolving the non-penetration constraint.
The depth of penetration can then be expressed as:
where δ would be positive if the bodies are separated and negative if the bodies are penetrating.
Hence, the position constraint function would be:
Velocity Constraint function
We can perform the time derivative of the above to get the velocity contraint function.
We can assume that the depth of penetration is small and ignore the second half of the equation, leaving us with:
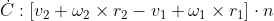
We want to isolate the velocity components from the above equation so that we can get the Jacobian. Things are a bit convoluted when working in 2D, as angular velocity is a scalar. If we consider the angular velocity as a 3d vector (since the scalar angular velocity can be considered as representing the magnitude of the angular velocity around the z-axis pointing out of the screen), we can use the following "hack" to change the cross product of ω and the radius r into the following matrix multiplication (remember, transpose of a skew-symmetric matrix is the negative of the original matrix and the cross product is ant-commutative, i.e. a x b = -(b x a)).
(I have borrowed the big-R notation from Dyn4j)
and with the above, the velocity equation can be re-written as:
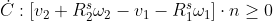
Separating the velocity components gives you:
Hence, by inspection the Jacobian matrix is:
Calculating the Impulse Magnitude
Remember that we want to calculate:
Relative velocity along the collision normal
Let's plug in the Jacobian for lambda, taking the first element of the numerator for starters.
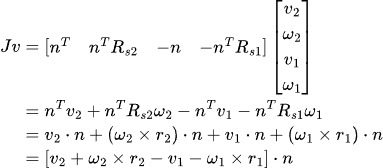
Similarly, plugging the Jacobian into the denominator part (effective mass) of the magic formula gives us:
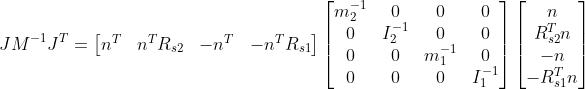
Effective Mass
Noting that the transpose of a matrix of matrices is the element wise transpose, and (AB)T = BTAT, plugging the Jacobian into the denominator part (effective mass) of the magic formula gives us:
Moving from left to right the first two matrices we obtain:
Working through the matrix multiplication again gives us:
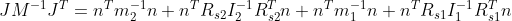
Since m is a scalar:
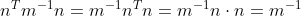
and I is also scalar, the effective equation can be rearranged as:
Breaking down the above into its elements, and looking at the third term in particular for easy analysis:
Hence the effective mass in 2D is:
Bias term
The bias velocity "vector" in constant constraints typically used for two things:
correct the position error - Baumgarte Stabilization term
to induce bounce - Restitution term
Baumgarte Stabilization
Applying impulse to "kill off" the relative velocity along the normal to zero is not enough. This will only prevent the two bodies from further penetrating. It does nothing to actually push them apart. For this you need to include something referred to as Baumgarte stabilization.
The basic idea is to feed the penetration depth (position error) back in as a bias velocity, or put another way, an extra bit of impulse is introduced into the system to push the two bodies apart. Such a bias velocity can be calculated as a multiple of the position constraint function error as follows.
where, β is the bias factor.
C is from the position constraint function, ie the measure of separation. The constraint comes into action only when it is not satisfied, ie when the bodies are colliding. So C in the above term would be negative. Some implementations will use the depth of penetration instead of the "separation", and in such cases the sign will be different.
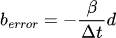
Penetration Slop
The Baumgarte stabilization will try to correct the position constraint error even if the error is very small, even if the two bodies are penetrating by just a very small distance, an extra impulse will be applied. This can result in unnecessary "jitter". This can occur pretty much every frame if say a body is sitting on the ground and gravity is acting upon it.
This type of situation can be improved by allowing a bit of "leeway" in the penetration before actually applying Baumgarte stabilization - this is referred to as penetration slop.
The penetration slop can be implemented as follows:
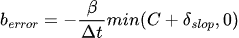
The effect is to reduce the Baumgarte term to zero if it is less than the penetration slop.
Again, you need to be careful about how you are feeding in the error term. If the depth of penetration is used, the formula then becomes:
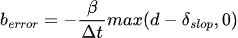
Restitution term
Box2D-Lite does not deal with bounce. However, bounce can be achieved by adding another bias term. In this case we need to introduce some velocity reflection when a contact occurs.
If vn' is the relative velocity after contact we want the following relative velocity.
where α is the restitution coefficient (if this is zero, there is no bounce).
This implies that:
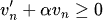
Hence, the restitution bias term is:
There is a presentation by Erin Catto here which describes how it should be done.
Calculating the impulse and the Δv
Now we can calculate lamda, by calculating lambda we can calculate Δv to resolve the non-penetration constraint, ie the collision!
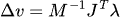
Useful References
This actually has code in Javascript
Lots of useful stuff available here
Comentarios