cedarcantab

Jun 20, 20225 min read

Understanding 2D Physics Engines with Phaser 3, Part 17.2: Collision Response with Rotation

Updated: Aug 17, 2023

Capsule to Capsule collision response with rotation

In the previous post I looked into how we can identify contact point(s) when two capsules collide. In this post, I finally look into calculating the collision response necessary to effect collision response with rotation.

Collision response: The Impulse Method

For now, we will ignore friction.

As such we are interested in finding the impulse to be applied along the collision normal to change the relative velocity.

We will first look at what happens to "velocity" when there is rotation.

Relative velocity

As with the collision response between two circles, we need to work with the relative velocity of the two capsules; specifically, the relative velocity at the point of contact and to find the relative velocity at the contact point, you obviously need to work out the velocity of capsule A at the contact point, and the velocity of capsule B at the contact point, then take the difference. But what velocity?

Linear Velocity

Up until now we have only talked about one velocity value. Strictly speaking, we have been referring to the linear velocity at the center of mass. When an object is not experiencing any rotation, the linear velocity at the center of mass is the same as the linear velocity at any other point of the object.

Angular Velocity

However, as you will intuitively recognize, when say, a circular plate is rotating without any linear motion, the point at the edge of the circle is moving at some pace, while the point at the center is actually not moving at all.

So how do we calculate the velocity at the contact point of a rotating object?

Velocity of a rotating body at the contact point

The linear velocity of point p of an object which is rotating is the sum of the linear velocity at its center of mass and the cross product of its angular velocity x vector from the center of mass to the contact point p.

So, the linear velocities of bodies A and B at the contact point P, before collision may be expressed as:

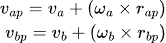
where:

v(ap) is the velocity of body A at point p
v(a) is the velocity of body A at its center of mass
ω(a) is the angular velocity of body A around the axis passing through its center of mass

and the equivalent velocity expressions after collision are:

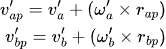
Armed with this knowledge we can go onto derive the formula for calculating the impulse.

Calculating the impulse

Recall that relative velocity when there is no rotation was defined as:

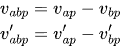
The rotational equivalent of the above are:

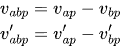
In a world of no ration, impulse method changes linear velocities by impulse J scaled by the inverse of their corresponding masses, m(a) and m(b). (Note that below assumes J is pointing from A to B)

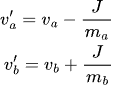
The rotational equivalent is:

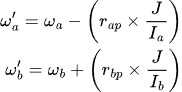
Impulse can be decomposed into components along the collision normal and tangent.

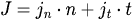
We can say that:

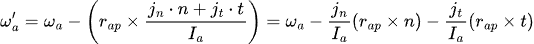
Similarly,

Note that the equation has been expanded to describe the change in angular velocities, casued by the normal and tangent compoenents of the impulse.

The corresponding equations describing the linear velocity changes are:

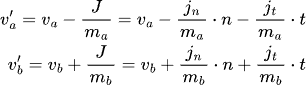
From the above, by substitution we get:

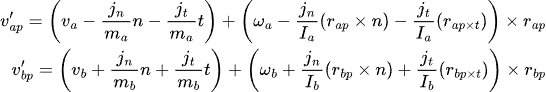
Ignore the contribution from the angular velocity tangent component as immaterial.

Then perform the dot product on both sides by n.

Which can be expanded to:

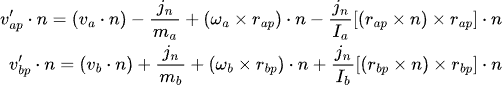
Let's look at the last part of this expression, and to make the analysis simpler, call D= r(ap) x n. Utilizing the scalar triple product identity (D x E)・F = D・ (E x F), we can say that:

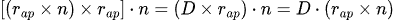
which means that:

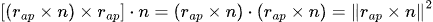
so,

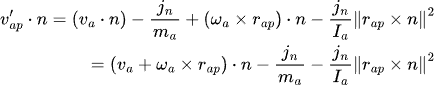
but recall that:

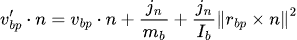
similarly,

Since v(abp)'=-e(v(abp)・ n):

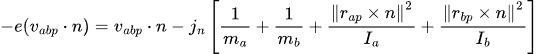
Collecting terms we get the following formula for calculating the magnitude of the impulse J along the collision normal:

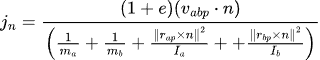
The necessary impulse for the collision response can be obtained by scaling the collision normal vector by the above.

Applying the Impulse

The impulse calculated above can then be substitued back into the respective post collision linear velocity and angular velocity formulae.

Effective Mass

We saw in a much earlier post covering circle to circle collision response (no rotation), the "impulse scalar" j is the relative velocity divided by the sum of the inverse masses.

The denominator of the big equation - referred to as the effective mass - is the sum of the inverse masses plus the rotational equivalents. The angular equivalent of mass is moment of inertia. We do not simply sum the inverse of the mmoi of the two bodies. It is important to note that the angular component of the denominator is not constant like with mass - it varies depending on the position of the contact point.

Working through the equations into code

Even with the information above, it was quite tricky to implement the code given the complexity of the equations, but I eventually ended up with this, which seems to give the correct result.

 responseCaps2Caps2(capsule1, capsule2, manifold) {
    
    let n = manifold.normal;
   
    // Calculate the pre-collision relative velocity at the point of contact 
    let r1 = new Phaser.Math.Vector2(manifold.points[0].x - capsule1.position.x, manifold.points[0].y-capsule1.position.y); // radii from COM to contact
    // calculate linear velocity component at contact point arising from angular velocity
    // effectively angular velocity cross radii, but in 2D simpler to rotate the radii and scale it by angular velocity
    let omega1 = new Phaser.Math.Vector2(-capsule1.angularVelocity * r1.y, capsule1.angularVelocity * r1.x);
    // calculate linear velocity of capsule 1 at contact point
    let v1 = capsule1.velocity.clone().add(omega1);
    // same calculations for capsule 2
    let r2 = new Phaser.Math.Vector2(manifold.points[1].x -capsule2.position.x, manifold.points[1].y-capsule2.position.y); // radii from COM to contact
    let omega2= new Phaser.Math.Vector2(-capsule2.angularVelocity * r2.y, capsule2.angularVelocity * r2.x);
    let v2 = capsule2.velocity.clone().add(omega2);
    
    let rv = v1.clone().subtract(v2); // relative velocity
    let rvn = rv.dot(n); // relative velocity along the collision normal

    // Calculate impulse
    let r1CrossN = r1.cross(n);
    let r2CrossN = r2.cross(n);
    
    let effectiveMass = capsule1.inv_m + capsule2.inv_m + r1CrossN*r1CrossN*capsule1.inv_inertia + r2CrossN*r2CrossN*capsule2.inv_inertia;
    
    let e =  Math.min(capsule1.restitution, capsule2.restitution);
    
    let j = -(1+e)*rvn / effectiveMass; // impulse scalar   
    let impulse = n.clone().scale(j); // impulse vector along the contact normal

    // Calculate post collision velocities
    capsule1.velocity.add(impulse.clone().scale(capsule1.inv_m));
    capsule2.velocity.subtract(impulse.clone().scale(capsule2.inv_m));

    capsule1.angularVelocity += capsule1.inv_inertia * r1.cross(impulse);
    capsule2.angularVelocity -= capsule2.inv_inertia * r2.cross(impulse); 
 
  }

Calculating the moment of inertia

The above assumes we have calculated the moment of inertia of the capsule. We have derived the formula for calculating this in the previous post.

It can be implemented as follows.

   calculateMass(density = 0.005) {
     
    let r2 = this.radius * this.radius;
    let w = Phaser.Geom.Line.Length(this); // w is the distance between the centres of the end circles
    let ra = this.height * w ; // area of the "rectangle";
    let rm = ra * density; // mass of the rectangle area
    let ca = Math.PI * r2 ; // area of the "circle area"
    let cm = ca * density ; // mass of the circle area
    this.area = ra + ca ; // total area of the capsule
    this.mass = rm + cm;  // total mass
    this.inv_m  = this.mass === 0 ? 0 : 1 / this.mass;
    // inertia is the rectangular region plus the inertia of the 2 half circles at a distance from centre of mass
    let d = w * 0.5; // distance of the centre of the "circle" from the centre of mass
    // parallel axis theorem I2 = Ic + m * d^2
    let cI = 0.5 * cm * r2 + cm * d * d;
    let rI = rm * (this.height * this.height + w * w) / 12;
    this.inertia = cI + rI;
    this.inv_inertia = this.mass === 0 ? 0 : 1 / this.inertia;
   
  }

For further study

This is pretty much the most basic form of collision response involving rotation. It took me a long time to get it working, but the satisfaction was great!