Physics Simulations in Javascript: Circle to Boundary Collision Detection
- cedarcantab
- Feb 4, 2022
- 5 min read
Updated: Jun 17, 2023
Boundary Collision Detection
Following on from the previous post, we introduce the concept of collision detection by discussing how to detect when a ball (circle) hits an edge of the screen (boundary).
We will also touch on collision separation and response, ie make the balls bounce off the boundaries so that they do not fly off the screen.
What is Collision Detection?
As the name suggests, collision detection is the process of detecting when an object has collided with another object. In the world of computer simulations this is the same as detecting when an object has intersected, penetrated, or overlapped with another object. For example, if you have two circles, we detect that they have collided if they have penetrated each other like below.
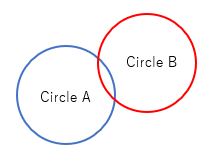
In the real world rigid body objects do not penetrate each other, but when you have objects moving around the screen, they can penetrate. Collision detection is synonymous with detecting penetrating objects.
In this post we are looking at how do detect when a ball has collided with a boundary. This is actually detecting the following type of penetration. From left to right, the figures illustrate a circle 'colliding' with the (i) right boundary edge, (ii) bottom boundary, (iii) left boundary, and (i) top boundary.
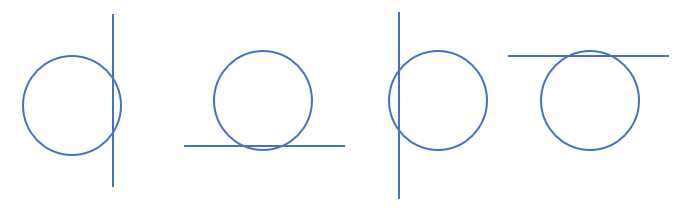
Collision Detection = Detecting Overlap
This collision detection is actually trying to assess when a circle has overlapped or intersected a line. More specifically, it is assessing intersection with an axis-aligned line, ie lines that are aligned with the x- or y-axes.
The easiest way to code this collision detection is to simply check for all the four specific situations above. For example, in situation (i), you check if the right most edge of circle (ie center of the circle + radius) is greater than the x-axis of the boundary (ie width of the screen)
And that's our very first collision detection algorithm!
Collision Resolution
Let's take this a step further and briefly discuss collision resolution. As mentioned above, a circle has collided with a wall when it has overlapped with a boundary. There are two aspects to the behavior of the circle post the collision:
collision resolution: in the real world objects do not overlap - hence this impossible situation must be resolved, ie the penetrating objects must be separated
collision response: after the objects have been separated, you typically want the objects to do something, like bounce off a vertical wall, or perhaps come to a dead stop if the ball hits the ground.
Let us consider the following situation where a ball is moving diagonally downwards and right towards the right boundary with an initial (pre-collision velocity) of v1. The ball then collides with the right wall. Then it bounces off moving diagonally downwards towards the left, with post-collision velocity of v2.
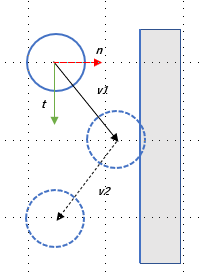
At this point we introduce the concepts of collision normal, collision tangent and depth of penetration - all critical concepts in coding physics simulation of colliding objects.
Collision Normal and Collision Tangent
Mathematically, we can decompose the initial velocity into the components that are perpendicular and parallel to the colliding wall. In general, the perpendicular direction to a collision is referred to as the collision normal (n), and the direction that is tangential to the collision position is the collision tangent (t). The vector v1 can be expressed as follows:
v1 = (v1 dot n) n + (v1 dot t) t
Depth of penetration
Another critical concept is the depth of penetration. This is the depth by which an object has penetrated the colliding object. More specifically it is the amount of overlap along the collision normal. In the case of the ball colliding against the right boundary, it is simply
right edge of the circle (center + radius) - x-coordinate of right boundary
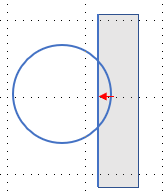
Separate the colliding objects
Once we have detected the ball has collided against the wall, we first need to separate it from the wall. We can do this simply by changing the position of the ball as follows:
position.x = position.x + depth of penetration
Collision Response, Bounce
In a perfect world with no friction and no loss of kinetic energy, a collision will not affect the components along the tangent direction while the normal component will simply be reversed.
The velocity post collision can be expressed as follows:
v2 = -(v1 dot n) n + (v1 dot t) t
Notice that the component along the collision normal has been reversed. In the real world some kinetic energy will be lost and magnitude of the post-collision velocity along the normal will be smaller than the pre-collision velocity along the normal.
It is relatively easy to implement 'bounciness' by introducing the concept of coefficient of restitution.
Coefficient of Restitution
Restitution basically describes how much energy is left after each collision. It has an effect on the bounciness of objects. The ratio between the starting and ending velocity after a bounce is called coefficient of restitution, or COR.
Objects with a COR of 0 would absorb all energy on impact, like a bag of sand hitting the floor.
Objects with a COR of 1 would have perfect elasticity, like a super bouncy bouncing ball.
Objects with a COR > 1 are completely fictional and would add extra energy after each collision.
By applying a certain COR to the post-collision velocity - specifically the component along the collision normal - we can simulate 'bounciness' making the objects lose a bit of energy after each bounce.
Coefficient of Friction
In a similar way we can implement friction by making the object "lose" a bit of any after each bounce by applying a coefficient of friction along the component of the velocity along the collision tangent, although we will not implement this for the demo in this post as it will make it unnecessarily complicated.
Implementation of Collision Detection, Collision Separation and Collision Response
The collision detection, separation and response can be implemented in 3 parts:
Check the balls x position against the left and right sides of the screen, the y position against the top and bottom of the screen, taking into account the size of the ball.
If the ball has gone "beyond" the edge of the screen, reset the ball's position so that it is just touching the edge of the screen.
The velocity of the ball along the collision normal is flipped to make the ball bounce off the wall.
collideWithBoundary(object) {
// collision detection of ball against all 4 sides of screen
const collision = {
left: (object.position.x - 0) < object.radius,
right: (SCREEN_WIDTH - object.position.x) < object.radius,
top: (object.position.y - 0) < object.radius,
bottom: (SCREEN_HEIGHT - object.position.y) < object.radius
}
// if there is any overlap, carry out overlap resolution
// then make the ball "bounce" in appropriate direction
if (collision.bottom) {
object.setPositionY(SCREEN_HEIGHT-object.radius)
object.velocity.y *= -object.restitution;
}
if (collision.top) {
object.setPositionY(0+object.radius);
object.velocity.y *= -object.restitution;
}
if (collision.left) {
object.setPositionX(0+object.radius)
object.velocity.x *= -object.restitution;
};
if (collision.right) {
object.setPositionX(SCREEN_WIDTH-object.radius)
object.velocity.x *= -object.restitution;
};
}And although simple, the above illustrates a lot of the most important principles of all collision detection routines. There is always: (i) collision detection, (ii) collision resolution, and (iii) collision response.
However, this is the most basic of collision detection routines in that: (i) the boundaries do not move, and significantly, (ii) the walls are aligned to the x and y axes; ie they are "axis-aligned".
Main Game Loop
In principle, the correct order for the main game loop is:
calculate the updated position of the objects,
carry out collision checks,
clear canvas, and
draw the objects.
In particular, the collision checks should be done straight after updating the positions so that the checks are carried out on the objects in their most recent state.
The update() method within the main scene is created as follows:
update (t, dt) {
this.dtinSeconds = dt/1000;
this.graphics.clear();
this.balls.forEach((ball) => {
ball.update(this.dtinSeconds);
this.collideWithBoundary(ball);
ball.render();
});
}And there we have it! We have created our very own physics engine! Albeit, very very very simple! If you check out the code below, you will see that Phaser arcade physics engine is not loaded in and the "work" is being done by the above code only!
References
I have referred to a number of different sources, including the following:

Comments