cedarcantab

May 26, 202213 min read

GJK in Javascript, Part 1: Detect Overlap Between Polygons

Updated: Apr 2

Collision Detection using Gilbert-Johnson-Keerthi (GJK) algorithm

Having looked at the Separating Axis Theorem (SAT), I look at another collision detection algorithm called the Gilbert-Johnson-Keerthi (GJK) algorithm. This is an algorithm that will detect overlap between any combination of convex shapes for which a support function (to be explained later) can be implemented.

In this post I will only touch lightly on the theory (refer to the Useful References for links to great documentation), focusing more on how I implemented it in Javascript.

Understanding the Jargon

Once you understand the basic logic behind GJK, you will appreciate the elegance of this algorithm and, in fact, its simplicity. Despite this simplicity it took me a long time to understand because of the many "technical" jargon that comes with the explanation of this algorithm. So before I go into my implementation explanation, here is the list of key words that you should have in your head if you wish to read through any material on this topic (the descriptions are mine interpretation and may not be mathematically accurate, but I think should help in the basic understanding of the GJK).

Minkowski Difference of two shapes: You flip one of the objects around the origin and add it to the other object. The resulting shape is the Minkowski Difference
Support Point: The most distant point in a given direction of the Minkowski Difference. It is the difference between the "extreme" points of the individual shapes. You can get it by passing the direction to the support function of one shape and the opposite direction to the other shape.
Support Function: A support function takes a direction vector and returns the support point on the Minkowski Difference.
Simplex: Refers to either a point, line segment, triangle or tetrahedron.
- 0-simplex is a point,
- 1-simplex is a line segment,
- 2-simplex is a triangle, and
- 3-simplex is a tetrahedron.

Basic idea behind GJK

The Minkowski Difference of two shapes will contain the origin (ie {x:0, y:0}), if the two shapes are intersecting.

Imagine a convex as being a cloud of points. Imagine two convex shapes A and B, being two clouds of points. On the other hand, Minkowski Difference is a collection points where each point is the result of a point from A plus the negative of a point from B. This is also referred to as Configuration Space Object (CSO).

If the shapes overlap, the two shapes will respectively contain the same point. By implication, if the shapes overlap, the Minkowski Difference will contain {x: 0, y: 0}, i.e. the origin. Theoretically if we can loop through all the points making up the Minkowski Difference and find that it contains the origin, the two shapes are overlapping. A shape is made up of an infinite number of points. It is not possible to search through an infinite number of points. GJK is an algorithm to efficiently confirm whether the Minkowski Difference contains the origin (or not), by iteratively consrtucting simplices.

The GJK iteratively creates a simplex (2-simplex, a triangle, in the case of 2D) from the support points until it finds a simplex that contains the origin.

The GJK is only interested in the "outer-hull" of the Minkowski Difference. More specifically, the outer-hull of a Minkowski Difference of two polygons (finite vertices) is made up of "extreme" points of the individual shapes - support points. It is simple to calculate this outer-hull of the Minkowski difference.

The basic steps are explained below.

First support point: 0-simplex

1. You start with the initial support point. To find a support point you provide the support function with a direction. For the first point, it does not really matter which direction you search. You can pick an arbitrary direction, say (1,0). Some implementations picks the vector pointing from the centre of one shape to the other.

Second support point: 1-simplex

2. You look for the next support by looking in the direction of the vector from the point just found to the origin.

3. Before you look for the next point, you check whether the second point has passed the origin. If the second support point is not past the previous support point, it means that there cannot be a simplex that contains the origin, so exit. Otherwise add the newly found point to the Simplex.

Third support point: 2-simplex

4. You look for the third point by getting the "normal" to the segment joining the first two points (remember the first two points lie on opposite sides of the origin), pointing towards the origin, then find the support point, thereby giving us a good chance of finding a triangle that contains the origin.

5. Once you have obtained 3 points, you have your first triangular simplex. Check whether the simplex contains the origin.

If the simplex contains the origin, you know that the polygons overlap.
If the simplex does not contain the origin, you need to look for the next simplex, like below.

Iteratively create simplex and check whether it contains origin

5. Find the vector that is perpendicular to the "edge" of the simplex that is closest to the origin, point it towards the origin and find the support point.

If you find that this support point has passed the origin, you get rid of one of the existing points, form the "next" simplex with the latest support point, and check whether the simplex contains the origin. If it does not, repeat.
If on the other hand, you find that this support point has not passed the origin, then we stop since there are no better simplices.

This site here has good visual explanation of how this is done.

Implementation in Javascript

Whilst the basic thinking behind GKJ is simple and elegant, there are many difficult implementation details, such as:

How do you find a support point of the Minkowski Difference?
How do you find that the "next" point is past the origin?
How do you find the support point in the direction of the perpendicular vector from a 1-simplex, i.e. a segment?
How do you determine that a triangle contains the origin?

Before we get into those implementation details we will create some base classes to make the coding easier.

Minkowski Difference class

Let's explore the Minkowski Difference in a bit more detail since this is the most important concept in GJK. We'll start with an explanation of the Minkowski Sum.

Let A and B be two shapes (2D or 3D), the Minkowski Sum of A and B, is a shape resulted from “sweeping” A all across the region occupied by B, or sweeping B across A (the result is the same). Another way of saying this is that the Minkowski Sum of A and B is a shape that is a cloud of points, where each point is the result of a point from A plus a point from B.

The GJK algorithm is only concerned with the outer hull of our cloud of vertices. More specifically, the algorithm only needs to identify the vertices of the Minkowski Difference, which in turn are the result of difference between "extreme" vertices of the two geometries, extreme being the furthest point in a given direction - such a point is referred to as a support point, and the function to identify such support points is referred to as a support function.

Support Point for a Minkowski Difference

The support point for a Minkowski Sum of two shapes can be expressed as the sum of the support points of individual shapes:

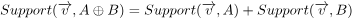
On the other hand, the support point for a Minkowski Difference (which is what we are interested in) is:

Note, you don't simply subtract the support point for B obtained by looking in the same direction as the support point for A. Note the negative before for the direction to be searched for the second shape in the above equation.

We can implement a class for a Minkowski Sum, together with a method for finding the support point.

class MinkowskiSum {

  constructor(shape1, shape2) {
    this.shape1 = shape1;
    this.shape2 = shape2;
  }

  getSupportPoint(direction) {
    
    // Find the support point by taking the farthest point in that direction of first shape and subtract the furthest point in the opposite direction of the second shape.
    var out = new Point()
    var point1 = this.shape1.getFarthestPoint(direction);
    var point2 = this.shape2.getFarthestPoint(direction.negate());
    direction.negate(); // put the direction back to the right direction
    return out.setTo(point1.x - point2.x, point1.y - point2.y);
	}

}

Note, getFarthestPoint is the suport functino for the releant convex shape. We have covered this in a separate post, here.

Having set up the basic classes, we now turn to the main GJK function

Main GJK loop - the set up

The main function will take 2 convex shapes as its parameters.

First create an array simplex to hold the simplex vertices.

Then we create a Minskowski Difference object from the 2 shapes.

detect(shape1, shape2) {
    
    var simplex = [];
    
    var ms = new MinkowskiSum(shape1, shape2);
    
    // main iteration loop
}

Having got the base classes in place, let's start looking at how we iteratively search through simplexes to find (or not) one that contains the origin.

Finding the 3 support points to build a 2-simplex

Finding the first support point

We start by seeding the simplex with an initial support point.

var d = this.getInitialDirection(shape1, shape2);
    // check for a zero direction vector
    if (d.isZero())) {
      d.set(1, 0);
    }

As stated earlier, to find the very first support point, we can look for the further point in an arbitrary direction.

In it convenient to have a function purely for getting the initial direction in which to look for the initial support point.

  getInitialDirection(shape1, shape2) {
      // Pick initial direction. Vector between the centeres of the two shapes
    return new Vector2(shape2.position.x - shape1.position.x, shape2.position.y-shape1.position.y);
  }

Then to get the first point, we simply look for the support point in the direction of the initial direction obtained from the above function, then add it to the simplex.

  // Pick first support point - first point on the smiplex
    simplex.push(ms.getSupportPoint( d))
    // negate the search direction
		d.negate();

Start of the iteration

With one point in the simplex array, we are now ready start the iterative search. The main iteration loop looks as follows.

   // start the loop
    for (let i = 0; i < 30; i++) {
 
        var supportPoint = ms.getSupportPoint(d);
        simplex.push(supportPoint);
            
        // make sure that the last point we added was past the origin
        if (supportPoint.dot(d) <= DEFAULT_DETECT_EPSILON) {
            // a is not past the origin so therefore the shapes do not intersect
            // here we treat the origin on the line as no intersection
            // immediately return with null indicating no penetration
            return false;
        } else {
            // if it is past the origin, then test whether the simplex contains the origin
            if (this.checkSimplex(simplex, d)) {
                // if the simplex contains the origin then we know that there is an intersection.
                // if we broke out of the loop then we know there was an intersection
                return true;
            }
            // if the simplex does not contain the origin then we need to loop using the new
            // search direction and simplex
        }
    }

The red highlighted code:

adds a support point
checks that the latest addition is past the origin (ie the previous point and the latest point straddle the origin)
if it the latest point is not past the origin, then we return false, we cannot possibly find a simplex that contains the origin

Having confirmed that the latest point straddles the origin vs the previous point, the main loops calls a method called checkSimplex whose parameters are:

the current simplex,
variable d, a Vector2 object (this is used to return the next direction in which to look for the next point, if necessary)

checkSimplex Function

The checkSimplex method returns true if the simplex contains the origin or sets d to the search direction for the next point.

The structure of the code looks as follows:

function checkSimplex(simplex, direction) {
   
    // get the last point added (a)
    var a = simplex[simplex.length - 1];
    // this is the same as a.to(ORIGIN);
    var ao = a.getNegative();
    // check to see what type of simplex we have


  if (simplex.length == 3) {
///// code to deal with triangle
}
else {
//// code to deal with segment
}
return false;
}

The function must deal with 2 types of simplices:

segment, ie 1-simplex, and
triangle, ie 2-simplex

Simplex is a segment

The code for dealing with a segment is reproduced below. Note, a is the most recently added point and b is the previously added point.

   else {
        // get the b point
        var b = simplex[0];
        var ab = a.to(b);
        
        direction.set(Vector2.tripleProduct(ab, ao, ab));
        // check for degenerate cases where the origin lies on the segment
        
        if (direction.getMagnitudeSquared() <= Epsilon.E) {
            // in this case just choose either normal (left or right)
            direction.set(ab.left());
        }
    }

To ease our understanding of the code above, imagine that we are in a situation like below where the red colored segment joining point A and point B represents the 1-simplex.

There are 3 voronoi regions that the origin could be in. However, since we started with B and searched towards the origin to end up with A, the origin cannot be region B. We have also confirmed that A is past the origin. Hence the origin cannot be in Region A. The origin must be in region AB, and the best direction in which to look for the next support point would be the perpendicular to segment AB.

We can find the perpendicular to a particular vector using the so called triple vector product, as below.

ACPerp = AB ⨯ (AB ⨯ AO)

Imagine you are looking at the above example on your PC screen. (AB x AO) will give you a vector pointing into the screen (remember the right hand rule where you index finger = a, your middle finger = b). Taking a cross product of the result with AB again gives you a vector that is orthogonal to the vector pointing into the screen and AB, pointing towards the origin.

Some implementations will use the following formula, in which case the vector will be pointing away from the origin.

ACPerp = AB ⨯ (AO ⨯ AB)

This can be implemented as follows.

static tripleProduct( a,  b,  c) {
		// expanded version of above formula
		var r = new Vector2();
			
		var dot = a.x * b.y - b.x * a.y;
		r.x = -c.y * dot;
		r.y = c.x * dot;
		
		return r;
	}
}

The above implementation makes use of the triple product expansion below.

a ⨯ (b ⨯ c) = b(a ⋅ c) - c(a ⋅ b)

Returning to the checkSimplex code, there is finally a check for the generate case. If A conincides with the origin, AO will be a zero vector. Or AB and AO are parallel (ie origin lies on AB). It means the shapes are just touching. You can decide if this is considered an overlap or not (in which case you can set the new vector as the perpendicular to AB).

Simplex is a triangle

Now let us delve into the most difficult part of this algorithm - how you deal with a triangle. Specifically, there are several implementation challenges:

How to determine if the triangle contains the origin (in which case, we return true, since there is overlap)
If the triangle does not contain the origin:
- How to look for direction in which to search for the next best point
- How to decide which point to throw out

The code is shown below. We will try to figure out what this is doing by working through an example.

  if (simplex.length == 3) {
        // then we have a triangle
        var b = simplex[1];
        var c = simplex[0];
        // get the edges
        var ab = a.to(b);
        var ac = a.to(c);
      
 	 // get the edge normal
      
        var acPerp = tripleProduct(ac, ab, ab);
        
        // see where the origin is at
        var acLocation = acPerp.dot(ao);
        if (acLocation >= 0.0) {
            simplex.splice(1,1);
            direction.set(acPerp);
        } else {
            // inlined Vector2.tripleProduct(ac, ab, ab) because
            // it can use dot from the tripleProduct(ab, ab, ac) above
            // see Vector2.tripleProduct implementation
            var abPerp = new Vector2();
            abPerp.x = ab.y * dot;
            abPerp.y = -ab.x * dot;
            
            var abLocation = abPerp.dot(ao);
            // the origin lies on the left side of A->C
            if (abLocation < 0.0) {
                // the origin lies on the right side of A->B and therefore in the
                // triangle, we have an intersection
                return true;
            } else {
                // the origin lies between A and B so remove C and set the
                // search direction to A->B perpendicular vector
                simplex.splice(0,1);
                // this used to be direction.set(Vector.tripleProduct(ab, ao, ab));
                // but was changed since the origin may lie on the segment created
                // by a -> b in which case would produce a zero vector normal
                // calculating ab's normal using c is more robust
                direction.set(abPerp);
            }
        }
    }

Let us imagine triangle ABC. Points were added to the simplex in the order C, B, and finally A.

To the human eye, it is easy to see that the triangle does not contain the origin. However to implement this in code basically requires you to check each of the different voronoi regions in turn. However, we do not need to check all the regions since each time we add a new point we check that the latest point straddles the origin vs the previous point, we can immediately say that the origin cannot be contained in regions A, B or C - leaving us to only check 4 out of the 7 voronoi regions.

Further, region BC cannot contain the origin because the new point we added point A, is supposed to be in the direction of the origin from edge BC.

This leaves us to test only 3 regions - we check these regions one by one.

Check again AC:

Check if the origin is "outside" the triangle against AC by looking at the direction of the perpendicular to edge AC - we can perform ABx(AC x AB) to yield the perpendicular vector to AC, ACPerp, pointing away from the origin.

Then we can perform ACPerp.dot(ao) to determine which side of AC the origin lies - the sign of this dot product will tell us on which side of AB the origin lies. If the result is positive, it means the origin lies on the "outside" (as in the above diagram) hence we need to drop one of the points and look for a better one. We know that the origin must lie between A and C, we drop B and set the new search direction to ACPerp.

On the otherhand, if the origin lies on the "inside" of AC, origin must lie in regions ABC or AB. So we must now check against AB.

Region AB:

We can calculate the perpendicular to AB, pointing away from the origin by:

ABPerp = AB x (AC x AB)

If ABPerp.dot(ao) is negative it means origin lies inside of AB in region ABC, ie the simplex contains the origin, so return true.

If the result is negative, it means the origin lies in region AB. Now throw away point C and set the new search direction to ABPerp.