Extending Phaser 3 Geom.Rectangle to Box2D-Lite, Part XX: Line Constraint

The line constraint is a constraint that restricts the movement of a pair of bodies to a prescribed "line". Dyn4j sites a car on a roller coaster track as being an example.

It is similar to the Prismatic constraint but the bodies are free to rotate about the anchor point.

The initial vector u will be supplied in the construction of the constraint.

From u, we will obtain the tangent of u, the t vector.

Each simulation step we will recompute u from the anchor points and use it along with the saved t vector to determine if the constraint has been violated.

class LineJoint extends Joint {
    constructor(b1, b2, anchor1 = b1.position, anchor2 = b2.position, dir, frequency = 30, dampingRatio = 1.0, jointMass = -1) {
        super(b1, b2, frequency, dampingRatio, jointMass);

        this.impulseSum = 0.0;
        if (body1.type == Type.Static && body2.type == Type.Static)
            throw "Can't make line constraint between static bodies";
        if (body1.type == Type.Dynamic && body2.type == Type.Dynamic)
            throw "Can't make line constraint between dynamic bodies";
        if (body2.type == Type.Static)
            throw "Please make line constraint by using the body1 as a static body";
 
        this.localAnchor1 = Vector2.InverseRotateAndTranslate(this.body1.Rot, this.body1.position, anchor1);
		this.localAnchor2 = Vector2.InverseRotateAndTranslate(this.body2.Rot, this.body2.position, anchor2);
        
        let u = anchor2.sub(anchor1);
        this.t = new Vector2(-u.y, u.x).normalized();
        if (dir == undefined) {
            let u = anchor2.sub(anchor1);
            this.t = new Vector2(-u.y, u.x).normalized();
        }
        else {
            this.t = new Vector2(-dir.y, dir.x).normalized();
        }
        Util.assert(this.t.squaredLength > 0);
    }

Position Constraint Function

The position constraint functino is defined as follows:

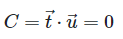
where

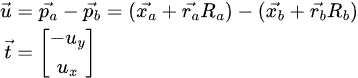
This equation states that any motion that is not along the vector is invalid, because the tangent of that motion projected onto (via the dot product) the t vector will no longer yield 0.

Velocity Constraint Function

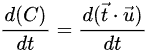
By the chain rule:

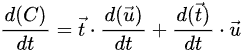
Where the derivative of u:

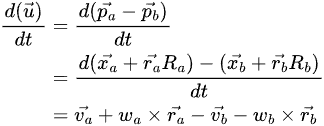
And the derivative of t:

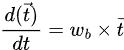
which gives us the following constraint function

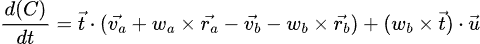
if we multiply this out, we get

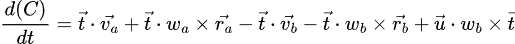
If we rely on the triple product identity, we can rearrange the above as

Isolate The Velocities

by inspection the jacobian is

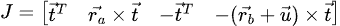
K-matrix

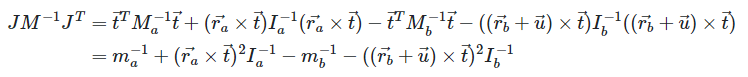
PreStep()

    preStep(inv_dt) {
        // Calculate Jacobian J and effective mass M
        // J = [-t^t, -(ra + u)×t, t^t, rb×t]
        // M = (J · M^-1 · J^t)^-1

        // Pre-compute anchors, mass matrix, and bias.
		Vector2.Rotate(this.body1.Rot, this.localAnchor1, this.r1);
		Vector2.Rotate(this.body2.Rot, this.localAnchor2, this.r2);

        let p1 = this.body1.position.add(this.r1);
        let p2 = this.body2.position.add(this.r2);
        this.u = p2.sub(p1);
        let k = this.body2.invMass + this.r2.cross(this.t) * this.body2.invI
            - (this.body1.invMass + this.r1.add(this.u).cross(this.t) * this.body1.invI)
            + this.gamma;
        this.m = 1.0 / k;
        let error = this.u.dot(this.t);
        if (Settings.positionCorrection)
            this.bias = error * this.beta * inv_dt;
        else
            this.bias = 0.0;
        if (Settings.warmStarting)
            this.applyImpulse(this.impulseSum);
    }

ApplyImpulse

  solve() {
        // Calculate corrective impulse: Pc
        // Pc = J^t · λ (λ: lagrangian multiplier)
        // λ = (J · M^-1 · J^t)^-1 ⋅ -(J·v+b)
        let jv = this.t.dot(this.body2.linearVelocity) + this.r2.cross(this.t) * this.body2.angularVelocity
            - (this.t.dot(this.body1.linearVelocity) + this.r2.add(this.u).cross(this.t) * this.body1.angularVelocity);
        let lambda = this.m * -(jv + this.bias + this.impulseSum * this.gamma);
        this.applyImpulse(lambda);
        if (Settings.warmStarting)
            this.impulseSum += lambda;
    }

Useful References

https://dyn4j.org/2010/12/line-constraint/