Extending Box2D-Lite in Javascript: Block Solver
- cedarcantab
- Aug 9, 2023
- 5 min read
Updated: Apr 6, 2024

We can solve a small number of constraints simultaneously to improve SI. For example, in 2D collision between convex shapes there is one or two contact points. In the case of two contact points, we can gain a lot of stability by solving both normal constraints simultaneously.
Inequality constraints can be active or inactive. An active contact point has a positive load while an inactive contact point has zero load. So with 2 contact points we have 4 cases. So first I try to solve both contact points as active. If one lambda is negative, I set lambda1 to zero and solve for lambda2. If lambda2 comes out negative, then I set lambda2 to zero and solve for lambda1. If lambda1 is negative then I set both lambdas to 0.

We stack the Jacobian for contact 1 and the Jacobian for contact 2 on top of each other, like so.
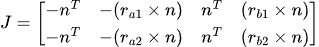
or, using the big-R notation from Dyn4j

where
\(ra1\) is the arm from center of mass of body A to contact point 1
\(rb1\) is the arm from center of mass of body B to contact point 1
\(ra2\) is the arm from center of mass of body A to contact point 2
\(rb2\) is the arm from center of mass of body B to contact point 2
K-matrix and Effective Mass
We start by calculating the K-matrix as usual K = (J · M^-1 · J^t)
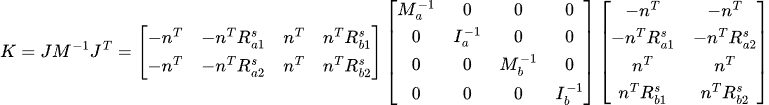
To make the analysis easier, let's define K as follows:

M = K^-1
4 cases
class BlockSolver {
constructor(manifold) {
this.manifold = manifold;
this.bodyA = manifold.bodyA;
this.bodyB = manifold.bodyB;
}
preStep() {
const manifold = this.manifold;
const mA = manifold.bodyA.invMass;
const mB = manifold.bodyB.invMass;
const iA = manifold.bodyA.invI;
const iB = manifold.bodyB.invI;
const normal = manifold.contacts[0].normal;
// Calculate Jacobian J and effective mass M
// J = [-n, -ra1 × n, n, rb1 × n
// -n, -ra2 × n, n, rb2 × n]
// K = (J · M^-1 · J^t)
// M = K^-1
// setup the block solver
let c1 = manifold.velocityConstraints[0];
let c2 = manifold.velocityConstraints[1];
let rn1A = c1.rA.cross(normal);
let rn1B = c1.rB.cross(normal);
let rn2A = c2.rA.cross(normal);
let rn2B = c2.rB.cross(normal);
// compute the K matrix for the constraints
this.k = new Mat22();
this.k.ex.x = mA + mB + iA * rn1A * rn1A + iB * rn1B * rn1B;
this.k.ey.x = mA + mB + iA * rn1A * rn2A + iB * rn1B * rn2B;
this.k.ex.y = this.k.ey.x;
this.k.ey.y = mA + mB + iA * rn2A * rn2A + iB * rn2B * rn2B;
this.m = this.k.invert();
}
solve() {
// if its 2 then solve the contacts simultaneously using a mini-LCP
// Block solver developed by Erin Cato and Dirk Gregorius (see Box2d).
// Build the mini LCP for this contact patch
//
// vn = A * x + b, vn >= 0, x >= 0 and vn_i * x_i = 0 with i = 1..2
//
// A = J * W * JT and J = ( -n, -r1 x n, n, r2 x n )
// b = vn_0 - velocityBias
//
// The system is solved using the "Total enumeration method" (s. Murty). The complementary constraint vn_i * x_i
// implies that we must have in any solution either vn_i = 0 or x_i = 0. So for the 2D contact problem the cases
// vn1 = 0 and vn2 = 0, x1 = 0 and x2 = 0, x1 = 0 and vn2 = 0, x2 = 0 and vn1 = 0 need to be tested. The first valid
// solution that satisfies the problem is chosen.
//
// In order to account for the accumulated impulse 'a' (because of the iterative nature of the solver which only requires
// that the accumulated impulse is clamped and not the incremental impulse) we change the impulse variable (x_i).
//
// Substitute:
//
// x = a + d
//
// a := old total impulse
// x := new total impulse
// d := incremental impulse
//
// For the current iteration we extend the formula for the incremental impulse
// to compute the new total impulse:
//
// vn = A * d + b
// = A * (x - a) + b
// = A * x + b - A * a
// = A * x + b'
// b' = b - A * a;
const manifold = this.manifold;
let c1 = manifold.velocityConstraints[0];
let c2 = manifold.velocityConstraints[1];
const N = manifold.contacts[0].normal;
// create a vector containing the current accumulated impulses
let a = new Vec2(c1.normalImpulse, c2.normalImpulse);
assert(a.x >= 0.0, a.y >= 0.0);
// get the relative velocity at both contacts and
// compute the relative velocities along the collision normal
let rv1 = Constraint.getRelativeVelocity(manifold.bodyA, manifold.bodyB, c1.rA, c1.rB);
let rv2 = Constraint.getRelativeVelocity(manifold.bodyA, manifold.bodyB, c2.rA, c2.rB);
let rvn1 = N.dot(rv1);
let rvn2 = N.dot(rv2);
// create the b vector
let b = new Vec2();
b.x = rvn1 - c1.velocityBias;
b.y = rvn2 - c2.velocityBias;
Vec2.Subtract(b, Mul(this.k, a), b )
for (;;) {
//
// Case 1: vn = 0
//
// 0 = A * x + b'
//
// Solve for x:
//
// x = - inv(A) * b'
//
let x = Mul(this.m, b).negate();
if (x.x >= 0.0 && x.y >= 0.0) {
this.applyImpulse( c1, c2, x, a);
break;
}
//
// Case 2: vn1 = 0 and x2 = 0
//
// 0 = a11 * x1 + a12 * 0 + b1'
// vn2 = a21 * x1 + a22 * 0 + b2'
//
x.x = -c1.normalMass * b.x;
x.y = 0.0;
rvn1 = 0.0;
rvn2 = this.k.ex.y * x.x + b.y;
if (x.x >= 0.0 && rvn2 >= 0.0) {
this.applyImpulse( c1, c2, x, a);
break;
}
//
// Case 3: vn2 = 0 and x1 = 0
//
// vn1 = a11 * 0 + a12 * x2 + b1'
// 0 = a21 * 0 + a22 * x2 + b2'
//
x.x = 0.0;
x.y = -c2.normalMass * b.y;
rvn1 = this.k.ey.x * x.y + b.x;
rvn2 = 0.0;
if (x.y >= 0.0 && rvn1 >= 0.0) {
this.applyImpulse( c1, c2, x, a);
break;
}
//
// Case 4: x1 = 0 and x2 = 0
//
// vn1 = b1
// vn2 = b2;
x.x = 0.0;
x.y = 0.0;
rvn1 = b.x;
rvn2 = b.y;
if (rvn1 >= 0.0 && rvn2 >= 0.0) {
this.applyImpulse( c1, c2, x, a);
break;
}
// No solution, give up. This is hit sometimes, but it doesn't seem to matter.
break;
}
}
applyImpulse(c1, c2, x, a) {
const manifold = this.manifold;
const mA = manifold.bodyA.invMass;
const mB = manifold.bodyB.invMass;
const iA = manifold.bodyA.invI;
const iB = manifold.bodyB.invI;
// V2 = V2' + M^-1 ⋅ Pc
// Pc = J^t ⋅ λ
const N = manifold.contacts[0].normal;
// find the incremental impulse
// Vector2 d = x.difference(a);
// apply the incremental impulse
let J1 = Vec2.Scale(N, x.x - a.x);
let J2 = Vec2.Scale(N, x.y - a.y);
let Jx = J1.x + J2.x;
let Jy = J1.y + J2.y;
manifold.bodyA.linearVelocity.subtractScaled(new Vec2(Jx, Jy), mA);
manifold.bodyA.angularVelocity -= iA * (c1.rA.cross(J1) + c2.rA.cross(J2));
manifold.bodyB.linearVelocity.addScaled(new Vec2(Jx, Jy), mB);
manifold.bodyB.angularVelocity += iB * (c1.rB.cross(J1) + c2.rB.cross(J2));
// set the new incremental impulse
c1.normalImpulse = x.x;
c2.normalImpulse = x.y;
}
}


Comments